Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vị trí tương đối của hai đường tròn (O ; R) và (O’ ; r) (R ≥ r) | Hệ thức giữa OO’ với R và r | Số điểm chung | |
|---|---|---|---|
Hai đường tròn cắt nhau | R – r < OO’ < R + r | 2 | |
Hai đường tròn tiếp xúc nhau | - Tiếp xúc ngoài | OO’ = R + r | 1 |
- Tiếp xúc trong | OO’ = R – r > 0 | ||
Hai đường tròn không giao nhau | - (O) và (O’) ở ngoài nhau | OO’ > R + r | 0 |
- (O) đựng (O’) | OO’ < R - r |
Còn lại phần cuối 0 bên phải nhá Ly yêu?

+ (O;R) đựng (O';r)(O′;r) có số điểm chung là 0; hệ thức giữa d,R,rd,R,r là d = R - r
+ (O;R) và (O';r)(O′;r) ở ngoài nhau có 0 điểm chung, hệ thức giữa d,R,rd,R,r là d > R + r
+ (O;R) và (O';r)(O′;r) Tiếp xúc ngoài có 1 điểm chung, hệ thức giữa d,R,rd,R,r là d = R + r
+ (O;R) và (O';r)(O′;r) Tiếp xúc trong có 1 điểm chung, hệ thức giữa d,R,rd,R,r là d = R - r
+ (O;R) và (O';r)(O′;r) cắt nhau có 2 điểm chung, hệ thức giữa d,R,rd,R,r là d < R + r
0; d<R-r
Ở ngoài nhau;0
1;d=R+r
Tiếp xúc trong;1
Cắt nhau;R-r<d<R+r

a) Dùng máy tính bỏ túi, tính các giá trị của S như sau:
Kết quả lần lượt là: 1,020703453
5,896455252
14,52201204
52,55287607
Ta được bảng sau:
| R (cm) | 0,57 | 1,37 | 2,15 | 4,09 |
| S= \(\pi R^2\) (cm2) | 1,02 | 5,89 | 14,52 | 52,55 |
b) Gỉa sử R' = 3R thế thì S' = \(\pi R'^2=\pi\left(3R\right)^2=\pi.9R^2=9S\)
Vậy diện tích tăng 9 lần.
c) \(79,5=S=\pi R^2\Rightarrow R^2=79,5:\pi\)
Do đó \(R=\sqrt{79,5:\pi}\approx5,03\left(cm\right)\)
Theo đúng quy tắc làm tròn đến 2 chữ số phần thập phân thì 5,896 \(\approx\) 5,90 nhé em.

| R | d | Vị trí tương đối của đường thẳng và đường tròn |
| 5cm | 2cm | Vì d<R nên đường thẳng cắt đường tròn. |
| 4cm | 4cm | Tiếp xúc nhau |
| 3dm | 7dm | Vì d>R nên đường thẳng và đường tròn không giao nhau. |
| R | d | vị trí tương đối của đường thẳng và đường tròn |
| 5cm | 2cm | cắt nhau |
| 4cm | 4cm | tiếp xúc nhau |
| 3dm | 7dm | không giao nhau |

Từ C = 2πR => R = ; C = πd => d=
.
Vậy dùng các công thức trên để tìm các giá trị chưa biết trong ô trống. Ta điền vào bảng sau:
|
Bán kính R của đường tròn |
10 |
(5) |
3 |
(1,5) |
(3,2) |
(4) |
|
Đường kính d của đường tròn |
(20) |
10 |
(6) |
3 |
(6,4) |
(8) |
|
Độ dài C của đường tròn |
(62,8) |
(31,4) |
(18,84) |
(9,42) |
20 |
25,12 |
Hướng dẫn giải:
Từ C = 2πR => R = ; C = πd => d=
.
Vậy dùng các công thức trên để tìm các giá trị chưa biết trong ô trống. Ta điền vào bảng sau:
|
Bán kính R của đường tròn |
10 |
(5) |
3 |
(1,5) |
(3,2) |
(4) |
|
Đường kính d của đường tròn |
(20) |
10 |
(6) |
3 |
(6,4) |
(8) |
|
Độ dài C của đường tròn |
(62,8) |
(31,4) |
(18,84) |
(9,42) |
20 |
25,12 |

a: 3x-y-1=0
=>y=-3x+1
(d)//(d') nên a=-3
b: \(4x+2y+3\sqrt{2}=0\)
=>\(2y=-4x-3\sqrt{2}\)
hay \(x=-2x-\dfrac{3\sqrt{2}}{2}\)
Để (d)vuông góc với (d') thì -2a=-1
=>a=1/2
c: Thay x=-1 và y=-2 vào (d), ta được:
-a+3=-2
=>3-a=-2
=>a=5

Hướng dẫn giải:
Vận dụng công thức: l = để tìm R hoặc no hoặc l. Thay số vào, tính toán ta tìm được các giá trị chưa biết trong ô trống và điền vào bảng sau:
|
Bán kính R của đường tròn |
10 cm |
(40,8 cm) |
21 cm |
6,2 cm |
(21cm) |
|
Số đo no của cung tròn |
90o |
50o |
(57o) |
41o |
25o |
|
Độ dài l của cung tròn |
(15,7 cm) |
35,6 cm |
20,8 cm |
(4,4cm) |
9,2 cm |
=
Vận dụng công thức: l = để tìm R hoặc no hoặc l. Thay số vào, tính toán ta tìm được các giá trị chưa biết trong ô trống và điền vào bảng sau:
|
Bán kính R của đường tròn |
10 cm |
(40,8 cm) |
21 cm |
6,2 cm |
(21cm) |
|
Số đo no của cung tròn |
90o |
50o |
(57o) |
41o |
25o |
|
Độ dài l của cung tròn |
(15,7 cm) |
35,6 cm |
20,8 cm |
(4,4cm) |
9,2 cm |

Bài giải:
Thực hiện phép tính và điền vào chỗ trống ta được bảng sau:
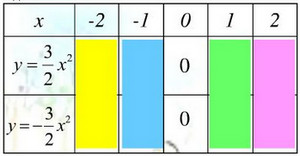
Vẽ đồ thị:
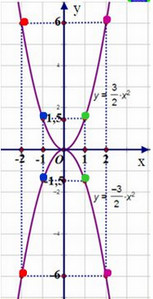
Nhận xét: Đồ thị của hai hàm số đối xứng với nhau qua trục Ox.
Xem thêm tại: http://loigiaihay.com/bai-4-trang-36-sgk-toan-9-tap-2-c44a5695.html#ixzz4dH45gBuO

1 watermelon
2 melon
3 pear
4 apple
5 grapes
6 lemon
7 orange
8 cái từ tomaao co viết sai ko nếu có thì là tomato đó xong rồi!
Ta có bảng sau: