Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow x\cdot\dfrac{3}{2}-\dfrac{780}{11}:\left[\dfrac{13}{15}+\dfrac{13}{35}+\dfrac{13}{63}+\dfrac{13}{99}\right]=-5\)
\(\Leftrightarrow x\cdot\dfrac{3}{2}-\dfrac{780}{11}:\left[\dfrac{13}{2}\left(\dfrac{2}{15}+\dfrac{2}{35}+\dfrac{2}{63}+\dfrac{2}{99}\right)\right]=-5\)
\(\Leftrightarrow x\cdot\dfrac{3}{2}-\dfrac{780}{11}:\left[\dfrac{13}{2}\left(\dfrac{1}{3}-\dfrac{1}{11}\right)\right]=-5\)
\(\Leftrightarrow x\cdot\dfrac{3}{2}-\dfrac{780}{11}:\dfrac{52}{33}=-5\)
\(\Leftrightarrow x\cdot\dfrac{3}{2}=40\)
hay x=40:3/2=80/3

= 18 x ( \(\dfrac{19}{21}\)+\(\dfrac{8}{9}\))+27 x \(\dfrac{17}{27}\)
=18 x \(\dfrac{113}{63}\)+27 x \(\dfrac{17}{27}\)
=\(\dfrac{226}{7}\)+17
=\(\dfrac{345}{7}\)
Chúc bạn học tốt!!

\(\Leftrightarrow\dfrac{2}{3x}-\dfrac{780}{11}:\left[13\left(\dfrac{1}{15}+\dfrac{1}{35}+\dfrac{1}{63}+\dfrac{1}{99}\right)\right]=-5\)
\(\Leftrightarrow\dfrac{2}{3x}-\dfrac{780}{11}:\left[\dfrac{13}{2}\left(\dfrac{2}{15}+\dfrac{2}{35}+\dfrac{2}{63}+\dfrac{2}{99}\right)\right]=-5\)
\(\Leftrightarrow\dfrac{2}{3x}-\dfrac{780}{11}:\left[\dfrac{13}{2}\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}\right)\right]=-5\)
\(\Leftrightarrow\dfrac{2}{3x}-\dfrac{780}{11}:\left[\dfrac{13}{2}\cdot\dfrac{8}{33}\right]=-5\)
\(\Leftrightarrow\dfrac{2}{3x}-45=-5\)
=>2/3x=40
=>3x=1/20
hay x=1/60

Ta có:
-21:7/28:4 = -3/4
-39:13/52:13 = -3/4
Vì -3/4 = -3/4 nên -21/28 = -39/52
-1717:101/2323:101 = -17/23
-171717:10101/232323:10101 = -17/23
Vì -17/23 = -17/23 nên -1717/2323 = -171717/232323

Ta có:\(\frac{1717}{9999}\)=\(\frac{17}{99}\)
\(\frac{171717}{999999}\)=\(\frac{17}{99}\)
Vậy cả 3 phân số đó đều bằng nhau.
chúng đều bằng nhau vì:
1717/9999=17/99 và 171717/999999=17/99
------------Thiên-------------

1)
a)
\(\dfrac{-21}{28}=\dfrac{\left(-21\right):7}{28:7}=\dfrac{-3}{4}\\ \dfrac{-39}{52}=\dfrac{\left(-39\right):13}{52:13}=\dfrac{-3}{4}\)
Vì \(\dfrac{-3}{4}=\dfrac{-3}{4}\) nên \(\dfrac{-21}{28}=\dfrac{-39}{52}\)
b)
\(\dfrac{-1717}{2323}=\dfrac{\left(-17\right)\cdot101}{23\cdot101}=\dfrac{-17}{23}\\ \dfrac{-171717}{232323}=\dfrac{\left(-17\right)\cdot10101}{23\cdot10101}=\dfrac{-17}{23}\)
Vì \(\dfrac{-17}{23}=\dfrac{-17}{23}\) nên \(\dfrac{-1717}{2323}=\dfrac{-171717}{232323}\)
2)
Theo tính chất cơ bản của phân số ta có: \(\dfrac{a}{b}=\dfrac{a\cdot m}{b\cdot m}\) mà \(m\ne n\)
nên không thể.
Trường hợp duy nhất là khi \(a=0\)
Khi đó: \(\dfrac{a}{b}=\dfrac{0}{b}=\dfrac{0\cdot m}{b\cdot n}=\dfrac{0}{b\cdot n}=0\)
3)
Gọi ƯCLN\(\left(12n+1,30n+2\right)\) là \(d\)
Ta có:
\(12n+1⋮d\\ \Rightarrow5\cdot\left(12n+1\right)⋮d\left(1\right)\\ \Leftrightarrow60n+5⋮d\\ 30n+2⋮d\\ \Rightarrow2\cdot\left(30n+2\right)⋮d\\ \Leftrightarrow60n+4⋮d\left(2\right)\)
Từ (1) và (2) ta có:
\(\left(60n+5\right)-\left(60n+4\right)⋮d\\ \Leftrightarrow1⋮d\\ \Rightarrow d=1\)
Vậy ƯCLN\(\left(12n+1,30n+2\right)=1\)
Mà hai số có ƯCLN = 1 thì hai số đó nguyên tố cùng nhau và không có ước chung nào khác
\(\Rightarrow\dfrac{12n+1}{30n+2}\)tối giản


\(A=\frac{5454}{5757}-\frac{171717}{191919}=\frac{54}{57}-\frac{17}{19}=\frac{54}{57}-\frac{51}{57}=\frac{3}{57}=\frac{1}{19}\)
\(\frac{5454}{5757}-\frac{171717}{191919}=\frac{54x101}{57x101}-\frac{17x10101}{19x10101}=\frac{54}{57}-\frac{17}{19}=\frac{1}{19}\)
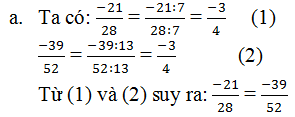

\(\left(\dfrac{17}{15}+\dfrac{17}{35}+\dfrac{17}{63}+\dfrac{17}{99}\right)\times\dfrac{11}{8}=\dfrac{68}{33}\times\dfrac{11}{8}=\dfrac{17}{6}\)
\(=\left(\dfrac{17}{15}+\dfrac{17}{35}+\dfrac{17}{63}+\dfrac{17}{99}\right):\dfrac{8}{11}=\dfrac{68}{33}\times\dfrac{11}{8}=\dfrac{748}{264}=\dfrac{17}{6}\)