Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
Phương pháp: Sử dụng giản đồ vecto
Cách giải:
Dựa vào đồ thị và dữ kiện đề bài:
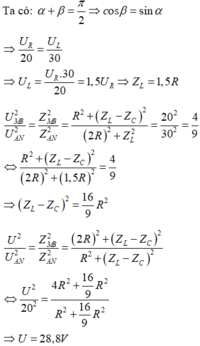

Đáp án A
Phương pháp: Áp dụng công thức tính công suất P = R I 2
Cách giải:
Công suất của mạch khi dòng điện trong mạch là 2 là P 1 = R . 2 2 = 4R
Công suất của mạch khi cường độ dòng điện trong mạch là 1 là
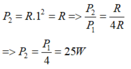

Tổng trở của mạch: \(Z=\frac{U}{I}=\frac{240}{\sqrt{3}}=80\sqrt{3}\left(\Omega\right)\)
\(Z_{MB}=\frac{80\sqrt{3}}{\sqrt{3}}=80\Omega\)
Ta có giản đồ véc tơ theo Z như sau:
i R Z Z Z r Z C AN L MB Z 80 80 80√3 80√2 45° 45° O
Từ giản đồ véc tơ ta có: \(Z_{AN}=80\sqrt{2}\)
Suy ra \(Z_C=80\)
Suy ra tam giác \(ORZ_{AN}\) vuông cân
\(\Rightarrow Z_LZ_{AN}Z_{MB}\) cũng vuông câ
\(\Rightarrow Z_L=80\cos45^0=40\sqrt{2}\)
Từ đó suy ra L

Đáp án C
Phương pháp: Mạch điện R, L, C mắc nối tiếp có ω thay đổi
Cách giải:
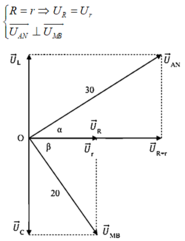
+ Khi ω = ω 0 công suất trên mạch đạt cực đại ω 0 2 = 1 L C P m ax = U 2 R = 732 ⇒ U 2 = 732 R ( * )
+ Khi ω = ω 1 và ω = ω 2 ; ω 1 – ω 2 = 120 π thì công suất tiêu thụ trên đoạn mạch bằng nhau:
P 1 = P 2 = P = 300 W ⇔ U 2 R R 2 + Z L 1 − Z C 1 2 = U 2 R R 2 + Z L 2 − Z C 2 2 ⇒ ω 1 ω 2 = 1 L C = ω 0 2
+ Ta có:
Z L 1 − Z C 1 = ω 1 L − 1 ω 1 C 1 = ω 1 L − 1 ω 0 2 ω 2 C = ω 1 L − ω 2 ω 0 2 C = ω 1 L − ω 2 1 L C C = ω 1 L − ω 2 L = ω 1 − ω 2 L = 120 π 1,6 π = 192
⇒ Z L 1 − Z C 1 = 192 ( ∗ ∗ )
+ Công suất tiêu thụ:
P = U 2 R R 2 + Z L 1 − Z C 1 2 = 300 ⇒ 300 R 2 + 300 Z L 1 − Z C 1 2 = U 2 R ( ∗ ∗ ∗ )
Từ (*) ; (**) ; (***) ⇒ 300 R 2 + 300.192 2 = 732 R 2 ⇒ R = 160 Ω

Đáp án A
n (vòng/phút) |
f |
ω |
Z L |
Z C |
|
2n (vòng/phút) |
2f |
2 ω |
2 Z L |
Z C 2 |
|
+ Khi tốc độ quay của roto là n (vòng/phút):
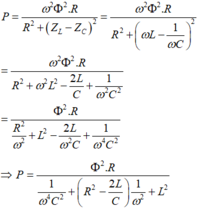
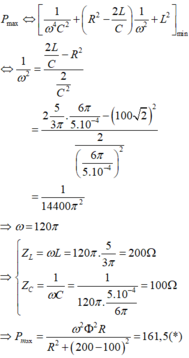
+ Khi tốc độ quay của roto là 2n (vòng/phút):