
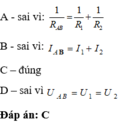
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

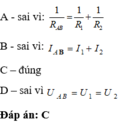

Cường độ dòng điện qua mạch chính
I = I1 + I2 = 4 + 2 =6 (A)
Điện trở R1 : \(R_1=\frac{U_1}{I_1}=\frac{U}{I_1}=\frac{120}{4}=30\Omega\)
Điện trở R2 : \(R_2=\frac{U_2}{I_2}=\frac{U}{I_2}=\frac{120}{2}=60\Omega\)
Điện trở mạch chính là
\(R=\frac{U}{I}=\frac{120}{6}=20\Omega\)
Công suất của mạch
\(P=\frac{U^2}{R}=\frac{120^2}{20}=720\left(W\right)\)

1, Câu A (vì để ko bị hỏng người ta chọn hiệu điện thế nhỏ nhất trong đoạn mạch)
2, Câu A (I toàn mạch sẽ bằng I1+I2=1A mà I=U/Rtđ => Rtđ= U/I=9/1=9Ω)
3,A ( Rtđ=(R1.R2)/R1+R2=8Ω =>I=U/Rtđ=3A;R1//R2 => U1=U2 mà R2=4R1 => I2=4I1 câu a hợp lý)
4,A ( Rtđ = U/I=24Ω. Ta có R1=2R2 ta lập phương trình: \(24=\frac{R2.2R2}{R2+2R2}=>R2=36;R1=2.36=72\)

a) Vì \(R_1\text{/}\text{/}R_2\text{/}\text{/}R_3\) nên: \(U=U_1=U_2=U_3\)
\(\Rightarrow\left\{{}\begin{matrix}I_1=\dfrac{U}{R_1}=\dfrac{24}{6}=4\left(A\right)\\I_2=\dfrac{U}{R_2}=\dfrac{24}{8}=3\left(A\right)\end{matrix}\right.\)
Vì \(R_1\text{/}\text{/}R_2\text{/}\text{/}R_3\) nên: \(I=I_1+I_2+I_3\)
\(\Rightarrow I_3=I-I_1-I_2=9-3-4=2\left(A\right)\)
\(\Rightarrow R_3=\dfrac{U}{I_3}=\dfrac{24}{2}=12\left(\Omega\right)\)
b) Điện trở tương đương của đoạn mạch là:
\(R_{TĐ}=\dfrac{U}{I}=\dfrac{24}{9}\approx2,667\left(\Omega\right)\)
Vậy .......................
a. Phân tích mạch: R1//R2//R3
+.Do R1//R2//R3 \(\Rightarrow\) I1= \(\dfrac{U}{R1}\) = \(\dfrac{24}{6}\)=4A (U=U1=U2)
I2=\(\dfrac{U}{R2}\)=\(\dfrac{24}{8}\)=3A (U=U1=U2)
I3=I-(I1+I2)=9-(4+3)=2A
+. R3=\(\dfrac{U}{I3}\)=\(\dfrac{24}{2}\)=12Ω
b.Vì R1//R2//R3\(\Rightarrow\)
Rtđ=\(\dfrac{R1.R2.R3}{R1+R2+R3}\)=\(\dfrac{6.8.12}{6+8+12}\)=\(\approx22\)

Ta có: U1=U; U2=2U; I1=I; I2=\(\dfrac{I}{2}\) (với U1,I1,U2,I2 lần lượt là hiệu điện thế và cường độ dòng chạy qua lần lượt điện trở R1, điện trở R2)
\(R_1=\dfrac{U_1}{I_1}=\dfrac{U}{I}\) ; \(R_2=\dfrac{U_2}{I_2}=\dfrac{2U}{\dfrac{I}{2}}=\dfrac{4U}{I}\)
\(\Rightarrow\dfrac{R_1}{R_2}=\dfrac{1}{4}\left(1\right)\)
Khi mắc R1 nối tiếp R2, hiệu điện thế ở 2 đầu mỗi điện trở tỉ lệ thuận với giá trị của chúng (cái này coi trong SGK)
Do đó \(\dfrac{U_1}{U_2}=\dfrac{R_1}{R_2}\)(2)
Lại có U1+U2=45 (vì R1 nt R2) \(\Rightarrow U_2=45-U_1\left(3\right)\)
Từ (1);(2);(3) ta có \(\dfrac{U_1}{45-U_1}=\dfrac{1}{4}\Rightarrow U_1=9\left(V\right)\Rightarrow U_2=45-9=36\left(V\right)\)

Tóm tắt :
R1 = 6\(\Omega\)
R2 = 10\(\Omega\)
R1 nt R2
U = 12V
a) Rtđ = ?
U = ?
b ) t = 40' = 2400s
A= ?
c) R3 // R1
R3 = ?; I = 1A
\(P_3=?\)
GIẢI :
a) Điện trở tương đương của đoạn mạch là :
\(R_{tđ}=R_1+R_2=6+10=16\left(\Omega\right)\)
Cường độ dòng điện qua đoạn mạch là :
\(I=\dfrac{U}{R_{tđ}}=\dfrac{12}{16}=0,75\left(A\right)\)
=> I1 = I2 = I = 0,75A (do R1 nt R2)
Hiệu điện thế giữa hai đầu điện trở R1 là :
\(U_1=I_1.R_1=0,75.6=4,5\left(V\right)\)
Hiệu điện thế giữa hai đầu điện trở R2 là :
\(U_2=I_2.R_2=0,75.10=7,5\left(V\right)\)
b) Nhiệt lượng tỏa ra của đoạn mạch trong 40 phút là:
\(Q=I^2.R.t=0,75^2.16.2400=21600\left(J\right)\)

ta có: R1= \(\dfrac{U}{I}\); R2= \(\dfrac{2U}{\dfrac{I}{2}}\)= \(\dfrac{4U}{I}\)
\(\Rightarrow\) \(\dfrac{R1}{R2}\)= \(\dfrac{U}{I}\): \(\dfrac{4U}{I}\)= \(\dfrac{1}{4}\)\(\Rightarrow\) R1= \(\dfrac{1}{4}\)R2
R1 nối tiếp R2
\(\Rightarrow\) I= I1=I2
\(\Rightarrow\) \(\dfrac{U1}{R1}\)= \(\dfrac{U2}{R2}\)
\(\Leftrightarrow\) \(\dfrac{U1}{0,25R2}\)= \(\dfrac{U2}{R2}\)
\(\Rightarrow\) \(\dfrac{U1}{U2}\)= \(\dfrac{1}{4}\)
mà U1+ U2= 45
\(\Rightarrow\) U1= 9( V)
U2= 36( V)

Tóm tắt :
\(I_1=3A\)
\(I_2=0,6A\)
\(R_1//R_2\)
_____________________________________
a) \(\dfrac{R_1}{R_3}=?\)
b) \(R_{tđ}=?\)
GIẢI :
a) Ta có : \(\left\{{}\begin{matrix}I_1=\dfrac{U}{R_1}\\I_2=\dfrac{U}{R_2}\end{matrix}\right.\)
=> \(\dfrac{I_1}{I_2}=\dfrac{R_2}{R_1}=\dfrac{3}{0,6}=5\)
=> \(R_2=5R_1\)
Vậy điện trở R2 có giá trị lớn hơn và lớn hơn 5 lần
b) Điện trở tương đương của mạch là :
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{R_1.5R_1}{R_1+5R_1}=\dfrac{5R_1^2}{6R_1}=\dfrac{5R_1}{6}\)
đối với đoạn mạch song song ta có
I1/I2=R2/R1 <=>
I2/I1=R1/R2=3/0,6=5 lần
=> I2>I1 và lớn hơn 5 lần
Tính Rtd theo R1
Rtd=(5R1×R1)/6R1