Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(U_C=I.Z_C=\dfrac{U.Z_C}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}.\omega C}=\dfrac{U}{\sqrt{\omega^2.C^2.R^2+(\omega^2.LC-1)^2}}\)
Suy ra khi \(\omega=0\) thì \(U_C=U\) \(\Rightarrow (1)\) là \(U_C\)
\(U_L=I.Z_L=\dfrac{U.Z_L}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U.\omega L}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}}=\dfrac{U.L}{\sqrt{\dfrac{R^2}{\omega^2}+(L-\dfrac{1}{\omega^2 C})^2}}\)(chia cả tử và mẫu cho \(\omega\))
Suy ra khi \(\omega\rightarrow \infty\) thì \(U_L\rightarrow U\) \(\Rightarrow (3) \) là \(U_L\)
Vậy chọn \(U_C,U_R,U_L\)
Chọn đáp án B
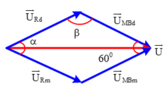
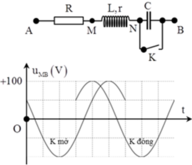
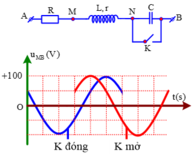
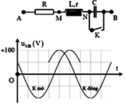
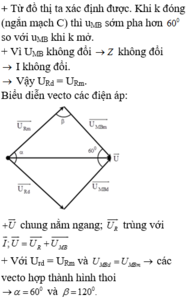
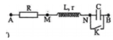
Khi K đóng (mạch gồm RLr) thì u M B sớm pha hơn 600 so với u M B khi K mở.
Vì 
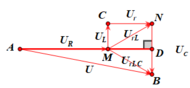
Điện áp AB không đổi 
nên ta có giản đồ vectơ các điện áp như hình bên.
Từ (1) và (2) 
Áp dụng định lý sin trong tam giác:
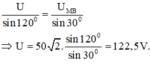
Đáp án D
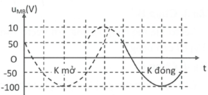
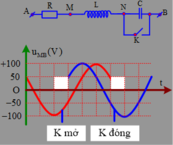
Trên đồ thị ta thấy: Khi K đóng u M B sớm pha hơn khi K mở góc π 3 và:
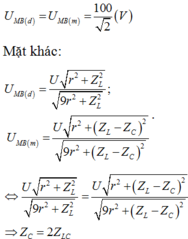
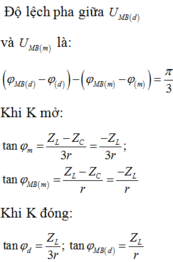
Thay vào biểu thức độ lệch pha trên, ta được:
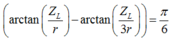
Lấy tan 2 vế, ta được:
Đáp án D
Từ đồ thị ta thấy điện áp hiệu dụng giữa hai điểm M và B trong hai trường hợp là bằng nhau và bằng 50 2 V . Pha ban đầu của điện áp u M B trong hai trường hợp mở và đóng là:
φ u M B − m o = π 3 φ u M B − d o n g = 2 π 3
Do đó, ta có: U M B 1 = U M B 2 ⇔ I 1 Z M B 1 = I 2 Z M B 2 ⇔ U Z 1 Z M B 1 = U Z 2 Z M B 2
⇔ r 2 + Z L − Z C 2 R + r 2 + Z L − Z C 2 = r 2 + Z L 2 R + r 2 + Z L 2 → R = 2 r r 2 + Z L − Z C 2 9 r 2 + Z L − Z C 2 = r 2 + Z L 2 9 r 2 + Z L 2 ⇒ Z L − Z C 2 = Z L 2 ⇒ Z L − Z C = − Z L ⇒ Z C = 2 Z L ⇒ Z d o n g = Z m o ⇒ I d o n g = I m o
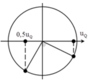
Chọn trục U làm chuẩn và nằm ngang, ta vẽ được giản đồ vectơ như hình:
Từ giản đồ véc tơ ta có: Δ A P B ~ Δ B P M ⇒ U L U r = U L + U r U L
Vì R = 2 r nên U R = 2 U r ⇒ U L = U r 3 ⇒ Z L = r 3
Lại có: U 2 M B = U r 2 + Z L 2 R + r 2 + Z L 2 ⇔ 50 2 = U r 2 + Z L 2 9 r 2 + Z L 2 → Z L = r 3 U = 50 6 V ≈ 122 , 4 V
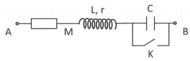
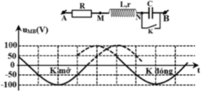
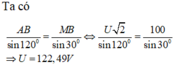
Đáp án A
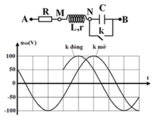
+ Từ đồ thị ta xác định được. Khi k đóng (ngắn mạch C) thì u MB sớm pha hơn 60 ° so với u MB khi k mở.
=> Áp dụng định lý hình sin trong tam giác, ta có: