
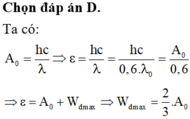
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

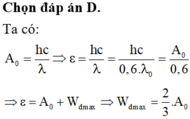

Giới hạn quang điện là bước sóng lớn nhất chiếu vào kim loại mà gây ra hiệu ứng quang điện phụ thuộc vào bản chất kim loại nên đáp án là B

Hệ thức Anh -xtanh trong hiện tượng quang điện
\(hf = A_1+W_{đ1}.(1)\)
\(hf = A_2+W_{đ2}.(2)\)
Ta có \(A_1 = \frac{hc}{\lambda_{01}}; A_2 = \frac{hc}{\lambda_{02}}\)
\( \lambda_{02} = 2\lambda_{01}=> A_1 = 2A_2. \)
Trừ vế với vế của phương trình (1) cho phương trình (2) ta có
=> \(0= A_1-A_2+W_{đ 1}-W_{đ 2}.\)
=> \(W_{đ2}=( A_1-A_2)+W_{đ1} = A_2+W_{đ1}\)
Mà \(A_2 >0\) => \(W_{đ2} > W_{đ1}\).

câu hỏi của bn có ở đây nhá Câu hỏi của HOC24 - Học và thi online với HOC24

Công thức Anh-xtanh cho hiện tượng quang điện ngoài
\(hf =A + \frac{1}{2} mv_{0max}^2= A+ W_{đmax}\)
=> \(\frac{hc}{\lambda_1} =\frac{hc}{\lambda_0}+W _{đmax1} \)
=> \(W_{đmax1} = \frac{hc}{\lambda_1} - \frac{hc}{\lambda_0} = 3,011.10^{-19}J.\)
Với công thoát: \(A = \frac{hc}{\lambda_0} = 3.011.10^{-19}J ; \frac{hc}{\lambda_1} = 6,023.10^{-19}J.\)
Mà \(v_{0max2} = \sqrt{2}v_{0max2} => W_{dmax1} = 2W_{dmax2} \)
=> \(\frac{hc}{\lambda_2} =\frac{hc}{\lambda_0}+W _{đmax2} = 3,011.10^{-19} + 6,023.10^{-19} = 9,035.10^{-19}J.\)
=> \(\lambda_2 =\frac{hc}{ \frac{hc}{\lambda_0} +W_{dmax2}} = \frac{6,625.10^{-34}.3.10^8}{9,035.10^{-19}} = 2,2.10^{-7}m = 0,22 \mu m.\)
Chọn đáp án.D. \(0,22\mu m.\)

Từ hệ thức Anh-xtanh ta có:
_ Với bức xạ \(\lambda_1:\)\(\frac{hc}{\lambda}=A+\frac{1}{2}mv^2_1\left(1\right)\)
_Với bức xạ \(\lambda_2:\)\(\frac{hc}{\lambda_2}=A+\frac{1}{2}mv^2_2\left(2\right)\)
Từ (1) và (2) \(\Rightarrow m_e=\frac{2hc}{v^1_2-v^2_2}\left(\frac{1}{\lambda_1}-\frac{1}{\lambda_2}\right)\)
![]()
ừ hệ thức Anh-xtanh ta có:
_ Với bức xạ λ1:hcλ=A+12mv21(1)λ1:hcλ=A+12mv12(1)
_Với bức xạ λ2:hcλ2=A+12mv22(2)λ2:hcλ2=A+12mv22(2)
Từ (1) và (2) ⇒me=2hcv21−v22(1λ1−1λ2)⇒me=2hcv12−v22(1λ1−1λ2).

Ta có
lấy tỉ lệ
1,5=\(\frac{hc}{1.2\lambda}\) => \(\lambda\)
sau đó A=\(\frac{hc}{\lambda}\)
không biết có đúng không. Nếu sai sót mong mn góp ý ạ![]()

1) Năng lượng 3,5 eV chính là công thoát A. Ta có:
\(A=3,5eV=5,6.10^{-19}J\)
Bước sóng ánh sáng cần chiếu vào kim loại chính là giới hạn quang điện ứng với kim loại đó:
\(\lambda_0=\frac{hc}{\lambda}=0,355\mu m\)
2) Khi dùng ánh sáng đơn sắc trên chiếu vào catôt của tế bào quang điện, năng lượng của phôtôn chỉ dùng để tạo công thoát A nên vận tốc ban đầu \(v_0\) của quang electron bằng 0. Dưới tác dụng của điện trường, công của lực điện trường tác dụng lên electron từ catôt đến anôt cung cấp cho electron động năng khi đến anôt:
\(\frac{mv^2}{2}=eU\); suy ra vận tốc electron khi đến anôt:
\(v=\sqrt{\frac{2eU}{m}}=4.10^6m\text{/}s\)

\(x_1=k_1\frac{\text{λ}_1D}{a}\)
\(x_2=k_2\frac{\text{λ}_2D}{a}\)
vân sáng của hai bức xạ bằng nhau \(\Leftrightarrow x_1=x_2\)
\(\Rightarrow\frac{k_1}{k_2}=\frac{\text{λ}_1}{\text{λ}_2}\Rightarrow\text{λ}_2=\frac{k_1\text{λ}_1}{k_2}=\frac{2.0,603}{3}=\text{0,402μm}\)
----> chọn A

Áp dụng: \(\varepsilon=A_t+W_đ\)
Năng lượng \(\varepsilon\) tỉ lệ nghịch với bước sóng
Động năng Wđ tỉ lệ thuận với bình phương vận tốc v
Suy ra:
\(\varepsilon =A_t+W_đ\)(1)
\(\dfrac{\varepsilon}{2} =A_t+\dfrac{W_đ}{k^2}\)(2)
\(\dfrac{\varepsilon}{4} =A_t+\dfrac{W_đ}{10^2}\)(3)
Lấy (1) trừ (2) vế với vế: \(\dfrac{\varepsilon}{2} =(1-\dfrac{1}{k^2})W_đ\)(4)
(1) trừ (3):\(\dfrac{3\varepsilon}{4} =\dfrac{99}{100}W_đ\)(5)
Lấy (4) chia (5) vế với vế: \(\dfrac{2}{3}=(1-\dfrac{1}{k^2}).\dfrac{99}{100}\)
\(\Rightarrow k=\sqrt{\dfrac{200}{97}}\)