Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giải thích: Đáp án A
Phương pháp:
- Áp dụng công thức tính vận tốc và quãng đường của vật trong chuyển động thẳng nhanh dần đều
- Áp dụng định luật II Niuton
Cách giải:
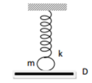
- Tần số góc: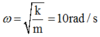 
- Vật chuyển động nhanh dần đều cùng ván, khi bắt đầu rời khỏi tấm ván, vận tốc và quãng đường vật đi
được lúc đó là: 
- Khi vật rời ván, áp lực do vật tác dụng lên ván bằng 0 nên chỉ còn lực đàn hồi và trọng lực tác dụng lên tấm ván.
ADĐL II Niuton ta được: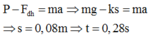 
Đáp án C
Giá ban đầu giữ cho lò xo không biến dạng sau đó giá bắt đầu chuyển động nhanh dần đều với gia tốc a.
Khi bắt đầu rời giá đỡ, vật đã đi được quãng đường S và gia tốc cũng là a:
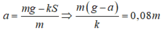
Thời gian tính đến lúc rời giá đỡ là:
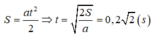
Tốc độ và độ lớn li độ của vật lúc rời giá đỡ là:
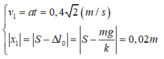
Biên độ dao động:
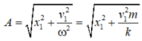
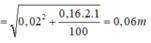
Chọn đáp ánC
Giá ban đầu giữ cho lò xo không biến dạng sau đó giá bắt đầu chuyển động nhanh dần đều với gia tốc a. Khi bắt đầu rời giá đỡ, vật đã đi được quãng đường S và gia tốc cũng là a:
a = m g − k S m ⇒ m ( g − a ) k = 0 , 08 m
Thời gian tính đến lúc rời giá đỡ là:
S = a t 2 2 ⇒ t = 2 S a = 0 , 2 2 ( s )
Tốc độ và độ lớn li độ của vật lúc rời giá đỡ là:
v = a t = 0 , 4 2 ( m / s ) x 1 = S − Δ l 0 = S − m g k = 0 , 02 m
Biên độ dao động:
A = x 1 2 + v 1 2 ω 2 = x 1 2 + v 1 2 m k = 0 , 02 2 + 0 , 16.2.1 100 = 0 , 06 m
Vận tốc của hai vật sau va chạm: (M + m)V = mv
=> V = 0,02\(\sqrt{2}\) (m/s)
Tọa độ ban đầu của hệ hai vật x0 = \(\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}\) = 0,04m = 4cm
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2+\left(M+m\right)}{k}=0,0016\Rightarrow A=0,04m=4cm\)
→ B
Vận tốc của hai vật sau va chạm: \(\left(M+m\right)V=mv\)
\(\rightarrow V=0,02\sqrt{2}\left(m\text{ /}s\right)\)
Tọa độ ban đầu của hệ hai vật: \(x_0=\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}=0,04m=4cm\)
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2\left(M+m\right)}{k}=0,0016\) \(\rightarrow A=0,04m=4cm\)
Đáp án B
Giải thích: Đáp án A
Phương pháp : Áp dụng định luật II Niuton, lí thuyết về chuyển động th ẳng nhanh dần đều , hê ̣thức độc lập theo thời gian của x vàv để tính biên độ. Áp dụng công thức tính vận tốc cực đại của con lắc lò xo dao động điều hoà.
Cách giải:
Viết phương trình 2 Niuton cho vật nặng ta được: P – N – Fđh = ma
Khi vật bắt đầu rời tấm ván thì N = 0. Khi đó : P – Fdh ma mg k l ma l 0, 08m 8cm
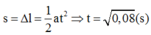
Với chuyển động nhanh dần đều có vận tốc đầu bằng 0 ta áp dụng công thức:
Ta có ω = 10 rad/s , vị trí cân bằng của vật lò xo dãn: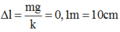 
Tại thời điểm vật rời ván ta có: x = -0,02m; 
Biên độ dao động: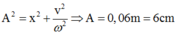 
Vận tốc cực đại của vât: 
Chọn B.
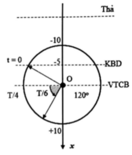
Độ dãn của lò xo ở vị trí cân bằng
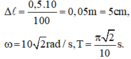
Chọn trục Ox thẳng đứng, hướng xuống, gốc O trùng vtcb. Các lực tác dụng vào vật khi chưa dời khoit giá đỡ: F Ð h → ; P → ; N → ''
Thả cho hệ rơi tự do nên Fđh = N (N là phản lực của giá đỡ tác dụng lên vật). Vật bắt đầu rời khỏi giá đỡ khi N = 0
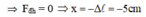
Như vậy, hệ đến vị trí lò xo không biến dạng thì vật sẽ tách ra khỏi giá => quãng đường vật đã đi được là S = 7,5 cm =0,075m => vận tốc tại vị trí tách:
Từ lúc vật bắt đầu dao động điều hòa (t = 0) sao T/4 thì thời gian mà lực đàn hồi và lực kéo về ngược chiều nhau = T 6 = π 2 60 s .
Giải thích: Đáp án A
Phương pháp: Sử dụng lí thuyết về dao động điều hòa của con lắc lò xo thẳng đứng
Cách giải:
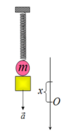
+ Khi cho giá đỡ chuyển động thì các lực tác dụng vào vật nặng của con lắc
Trọng lực, lực đàn hồi, phản lực do giá đỡ tác dụng lên vật
Theo định luật II Niu-tơn ta có: 
Chiếu lên chiều dương là chiều chuyển động đi xuống của vật ta có:
+ Giá đỡ rời vật khi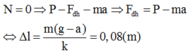 
Hay giá đỡ rời vật khi lò xo giãn đoạn 8 cm, mà độ giãn của lò xo ở VTCB
=> Vật đang ở vị trí có li độ x = - 2 cm
+ Vận tốc của vật tại vị trí đó là 
+ Tần số góc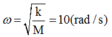 
=> Vật sẽ dao động với biên độ 
Chọn A
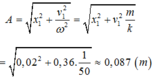
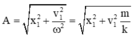
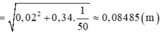
Chọn D
Vật rời khỏi giá đỡ khi phản lực N = 0
Áp dụng định luật II Newton cho vật trên ván chuyển động có gia tốc a, ta được:
mg – N – Fđh = ma
Vật rời ván khi N = 0→Fđh = k.∆l = m(g-a)→∆l = 9cm
Ban đầu ván ở vị trí lò xo giãn 1cm nên khi vật rời ván, ván đi được:
S = ∆l – 1 = 8cm
Khi đó tốc độ của vật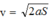
vật cách VTCB là 1cm (chiều dương hướng xuống → x = 1cm)
=>Biên độ dao động của vật: