
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

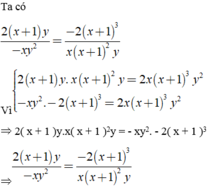

a) \(N=\left(x-5\right)\left(x+2\right)+3\left(x-2\right)\left(x+2\right)-\left(3x-\dfrac{1}{2}x^2\right)+5x^2\)
\(=x^2+2x-5x-10+3x^2-12-3x+\dfrac{1}{2}x^2+5x^2\)
\(=\dfrac{19}{2}x^2-6x-22\)
Vậy biểu thức trên phụ thuộc vào biến x.
b) \(\left(y-1\right)\left(y^2+y+1\right)=y^3-1\)
Giải:
VT = \(\left(y-1\right)\left(y^2+y+1\right)\)
\(=y^3+y^2+y-y^2-y-1\)
\(=y^3-1\)
Vậy \(\left(y-1\right)\left(y^2+y+1\right)=y^3-1\).
Giải:
a) \(N=\left(x-5\right)\left(x+2\right)+3\left(x-2\right)\left(x+2\right)-\left(3x-\dfrac{1}{2}x^2\right)+5x^2\)
\(\Leftrightarrow N=x^2-3x-10+3\left(x^2-4\right)-3x+\dfrac{1}{2}x^2+5x^2\)
\(\Leftrightarrow N=x^2-3x-10+3x^2-12x-3x+\dfrac{1}{2}x^2+5x^2\)
\(\Leftrightarrow N=-10-18x+\dfrac{19}{2}x^2\)
Vậy biểu thức trên phụ thuộc vào biễn x
b) \(\left(y-1\right)\left(y^2+y+1\right)\)
\(=y^3-y^2+y^2-y+y-1\)
\(=y^3-\left(y^2-y^2\right)-\left(y-y\right)-1\)
\(=y^3-1\)
Vậy ...

Ta có: \(\frac{x^2y+2xy^2+y^3}{2x^2+xy-y^2}\)
\(=\frac{x^2y+xy^2+xy^2+y^3}{2x^2+2xy-xy-y^2}\)
\(=\frac{xy\left(x+y\right)+y^2\left(x+y\right)}{2x\left(x+y\right)-y\left(x+y\right)}\)
\(=\frac{\left(x+y\right)\left(xy+y^2\right)}{\left(2x-y\right)\left(x+y\right)}=\frac{xy+y^2}{2x-y}\left(đpcm\right)\)
Ta có: \(\frac{x^2+3xy+2y^2}{x^3+2x^2y-xy^2-2y^3}\)
\(=\frac{x^2+xy+2xy+2y^2}{x^2\left(x+2y\right)-y^2\left(x+2y\right)}\)
\(=\frac{x\left(x+y\right)+2y\left(x+y\right)}{\left(x^2-y^2\right)\left(x+2y\right)}\)
\(=\frac{\left(x+2y\right)\left(x+y\right)}{\left(x+y\right)\left(x-y\right)\left(x+2y\right)}=\frac{1}{x-y}\left(đpcm\right)\)

Biến thì khác nhau nhưng quan trọng là cách làm :))
Vào TKHĐ của tớ để xem hình ảnh nhé, dài ngại chả muốn viết :V





Nếu chữ z là số 2 thì
2(x+1)(y+1) - (x+y)(x+y+z) = -x2 -y2 + 2 = 0
Vậy đẳng thức đúng

1) \(VT=x^3+x^2y-x^2y-xy^2+xy^2+y^3=x^3+y^3=VP\)
2) \(VP=x^2+xy-xy-y^2=x^2-y^2=VT\)
3) \(VP=x^2+2\cdot x\cdot1+1=x^2+2x+1=VT\)
4) \(VP=x^3+x^2y+xy^2-x^2y-xy^2-y^3=x^3-y^3=VT\)
1, \(\left(x^2-xy+y^2\right)\left(x+y\right)=x^3+y^3\\ x^3+x^2y-x^2y-xy^2+xy^2+y^3=x^3+y^3\\ x^3+y^3=x^3+y^3\left(đúng\right)\)Vậy ta được đpcm
2, \(x^2-y^2=\left(x-y\right)\left(x+y\right)\\ x^2-y^2=x^2+xy-xy-y^2\\ x^2-y^2=x^2-y^2\left(đúng\right)\)Vậy ta được đpcm
3, \(x^2+2x+1=\left(x+1\right)^2\\ x^2+2x+1=\left(x+1\right)\left(x+1\right)\\ x^2+2x+1=x^2+x+x+1\\ x^2+2x+1=x^2+2x+1\left(đúng\right)\)Vậy ta được đpcm
4, \(x^3-y^3=\left(x-y\right)\left(x^2+xy+y^2\right)\\ x^3-y^3=x^3+x^2y+xy^2-x^2y-xy^2-y^3\\ x^3-y^3=x^3-y^3\left(đúng\right)\)Vậy ta được đpcm

=(x4 -y4) +(x4+x2y2) + 3y2
= (x2+y2)(x2-y2) + x2(x2-y2) +3y2 = 3(dpcm)