

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Thử coi ạ, sai bỏ qua nha :))
a/ \(E_{tc}=L.\frac{\left|\Delta i\right|}{\Delta t}=0,5.\frac{0,4}{0,15}=\frac{4}{3}\left(V\right)\)
b/ \(I=\frac{E_{tc}}{R}=\frac{\frac{4}{3}}{0,5}=\frac{8}{3}\left(A\right)\)

a/ \(\phi=N.BS\cos\left(\overrightarrow{B};\overrightarrow{n}\right)=200.10^{-4}.20.10^{-4}.\cos30^0=2\sqrt{3}.10^{-5}\left(T.m^2\right)\)
b/ \(E_c=\left|\frac{\Delta\phi}{\Delta t}\right|=\left|\frac{-2\sqrt{3}.10^{-5}}{0,01}\right|=2\sqrt{3}.10^{-3}\left(V\right)\)
\(Q=\frac{E_c^2}{R}t=\frac{\left(2\sqrt{3}.10^{-3}\right)^2}{10}.0,01=12.10^{-9}\left(J\right)\)
c/ \(I=\frac{E_c}{R+R'}=\frac{2\sqrt{3}.10^{-3}}{10+2}=\frac{\sqrt{3}.10^{-3}}{6}\left(A\right)\)
Check lại phần tính toán hộ mình nhé, nhiều số quá hơi nhức mắt :(

a) Để công suất tiêu thụ mạch ngoài là lớn nhất thì R+X=r
=> X=1,1 - 0,1=1(\(\Omega\)
b) Để công suất tiêu thụ ở điện trở này là lớn nhất thì X=R+r =1,1+0,1=1,2\(\Omega\)
Công suất đó là: Pmax =I2.R=\(\left(\frac{\in}{R+X+r}\right)^2.X=\left(\frac{12}{1,1+1,2+0,1}\right)^2.1,2=30\left(\text{W}\right)\)

a) Tính điện trở x để công suất tiêu thụ ở mạch ngoài là lớn nhất.
- Mạch ngoài gồm điện trở R mắc nối tiếp với điện trở x, có điện trở tương đương là: RN = R + x = 0,1 + x.
- Cường độ dòng điện trong trong mạch : I = ξ/ (R + r + x)
- Công suất tiêu thụ mạch ngoài:

Để công suất P trên đây lớn nhất thì mẫu số ở về phải là nhỏ nhát. từ bất đẳng thức cô si ta có R + x = r.
Từ đó suy ra: x = r –R = 1 Ω.
b) Công suất tiêu thụ trên điện trở x:
- Tính công suất tiêu thụ trên điện trở x này là lớn nhất:
+ Từ các tính toán trên, ta có công suất tiêu thu, điện trở x là:
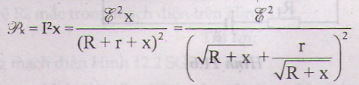
+ Tương tự như đã làm ở trên đây, công suất Px lớn nhất khi x= R + r = 1,2 Ω.
Giá trị của công suất lớn nhất này là:30 W.