Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E 6 H
a) BC = \(\sqrt{AB^2+AC^2}\)= \(\sqrt{6^2+8^2}\)= \(\sqrt{100}\)= 10 (theo định lí Pythagoras)
\(\Delta\)ABC có BD là phân giác => \(\frac{AD}{AB}\)= \(\frac{CD}{BC}\)= \(\frac{AD}{DC}\)= \(\frac{AB}{BC}\)= \(\frac{6}{10}\)= \(\frac{3}{5}\).
b) Ta có : \(\widehat{ABE}\)= \(\widehat{EBC}\)(BD là phân giác)
=> \(\Delta ABD\)~ \(\Delta EBC\)(gg)
=> \(\frac{BD}{BC}\)= \(\frac{AD}{EC}\)<=> BD.EC = AD.BC (đpcm).
c) Ta có : \(\Delta CHE\)~ \(\Delta CEB\)( 2 tam giác vuông có chung góc C )
=> \(\frac{CH}{CE}\)= \(\frac{CE}{CB}\)<=> CH.CB = CE2 (1)
\(\Delta CDE\)~ \(\Delta BDA\)(gg (2 góc đối đỉnh))
\(\Delta BDA~\Delta BCE\) (câu b))
=> \(\Delta CDE~\Delta BCE\)
=> \(\frac{CE}{BE}\)= \(\frac{DE}{CE}\)<=> BE.DE = CE2 (2)
Từ (1) và (2) => CH.CB = ED.EB (đpcm).

a) Gợi ý: Lập tỉ số các cặp cạnh tương ứng và chứng minh chúng bằng nhau.
b) Từ phần a 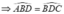 Þ ĐPCM
Þ ĐPCM

A B C D 8 10 20 25
a, - Vẽ điểm A: Vẽ cung tròn tâm B có bán kính = 4cm và cung tròn tâm D có bán kính = 8cm. Giao điểm của hai cung tròn này là điểm A.
Nối DA và BA.
Vậy là ta đã vẽ được tứ giác ABCD thỏa mãn điều kiện đề bài.
b, Ta có :
\(\frac{AB}{CD}=\frac{4}{10}=\frac{2}{5};\frac{BD}{CD}=\frac{10}{25}=\frac{2}{5};\frac{AD}{BC}=\frac{8}{20}=\frac{2}{5}\)
\(\Rightarrow\frac{AB}{BD}=\frac{BD}{DC}=\frac{AD}{BC}\Rightarrow\Delta ABD~\Delta BDC\left(c-c-c\right)\)
c, \(\Delta ABD~\Delta BDC\)
\(\Rightarrow\widehat{ABD}=\widehat{BDC}\)
Vì 2 góc này so le trong nên
=> AB // DC hay ABCD là hình thang
Vì ΔABD ⁓ ΔBDC nên A B B D = B D D C = A D B C , tức là 2 B D = B D 8 = 3 B C
Ta có B D 2 = 2.8 = 16 nên BD = 4 cm
Suy ra BC = 8.3 4 = 6 cm
Vậy BD = 4cm, BC = 6cm
Đáp án: D