K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
30 tháng 8 2018
Cho tứ diện ABCD có thể tích là V. Điểm M thay đổi trong tam giác BCD. Các đường thẳng qua M và song song với AB, AC, AD lần lượt cắt các mặt phẳng (ACD), (ABD), (ABC) tại N, P, Q. Giá trị lớn nhất của khối MNPQ là: A.  V 27 B.  V 16 C. V 8 .  D. ...
Đọc tiếp

Cho tứ diện ABCD có thể tích là V. Điểm M thay đổi trong tam giác BCD. Các đường thẳng qua M và song song với AB, AC, AD lần lượt cắt các mặt phẳng (ACD), (ABD), (ABC) tại N, P, Q. Giá trị lớn nhất của khối MNPQ là:

A.  V 27

B.  V 16

C. V 8 . 

D. V 54 .
#Mẫu giáo
1
CM
Cao Minh Tâm
30 tháng 8 2018

Đáp án A

Đúng(0)
PT
Pham Trong Bach
13 tháng 1 2018
Cho tứ diện ABCD có thể tích là V. Điểm M thay đổi trong tam giác BCD Các đường thẳng qua M và song song với A B , A C , A D  lần lượt cắt các mặt phẳng A C D , A B D , A B ...
Đọc tiếp

Cho tứ diện ABCD có thể tích là V. Điểm M thay đổi trong tam giác BCD Các đường thẳng qua M và song song với A B , A C , A D  lần lượt cắt các mặt phẳng A C D , A B D , A B C  tại N;P;Q. Giá trị lớn nhất của thể tích khối đa diện MNPQ là

A. V/27

B. V/16 

C. V/8

D. V/18
#Mẫu giáo
1
CM
Cao Minh Tâm
13 tháng 1 2018

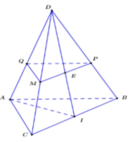
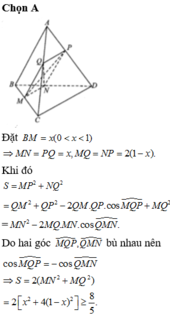
Đáp án A

Giả sử tứ diện ABCD có AB;AC'AD đội một vuông góc  ⇒ V A B C D = A B . A C . A D 6

Khi đó tứ diện MNPQ có MN;MP;MQ đội một vuông góc  ⇒ V M . N P Q = M N . M P . M Q 6

Ta chứng minh được M N A B + M P A C + M Q A D = 1  ( dựa vào định lý Thalet), khi đó

M N . M P . M Q = A B . A C . A D . M N A B . M P A C . M Q A D ≤ A B . A C . A D . M N A B + M P A C + M Q A D 3 27 = A B . A C . A D 27

Vậy  V M . N P Q = M N . M P . M Q 6 ≤ 1 27 . A B . A C . A D 6 = V 27 → V max = V 27

Đúng(0)
PT
Pham Trong Bach
23 tháng 8 2017
Cho tứ diện ABCD có AB vuông góc với CD, AB=CD=6. M là điểm thuộc canh BC sao cho MC=x.BC (0<x<1). Mặt phẳng (P) đi qua M và song song với AB và CD lần lượt cắt BC, DB, AD, AC tại M, N, P, Q. Diện tích lớn nhất S m a x của tứ giác MNPQ bằng bao nhiêu? A. 9 B. 4,5 C. 36 D. 18...
Đọc tiếp

Cho tứ diện ABCD có AB vuông góc với CD, AB=CD=6. M là điểm thuộc canh BC sao cho MC=x.BC (0<x<1). Mặt phẳng (P) đi qua M và song song với AB và CD lần lượt cắt BC, DB, AD, AC tại M, N, P, Q. Diện tích lớn nhất S m a x của tứ giác MNPQ bằng bao nhiêu?

A. 9

B. 4,5

C. 36

D. 18
#Mẫu giáo
1
CM
Cao Minh Tâm
23 tháng 8 2017

Chọn A

Đúng(0)
PT
Pham Trong Bach
4 tháng 1 2018
Cho tứ diện đều ABCD cạnh bằng 1. Xét các điểm M và N thay đổi lần lượt thuộc các cạnh AD, BC sao cho AM=CN=x (0<x<1). Gọi (P) là mặt phẳng chứa MN và song song với CD. Thiết diện của tứ diện với mặt phẳng (P) có diện tích nhỏ nhất bằng A.  1 4 B.  1 2 C.  3 4 D.  ...
Đọc tiếp

Cho tứ diện đều ABCD cạnh bằng 1. Xét các điểm M và N thay đổi lần lượt thuộc các cạnh AD, BC sao cho AM=CN=x (0<x<1). Gọi (P) là mặt phẳng chứa MN và song song với CD. Thiết diện của tứ diện với mặt phẳng (P) có diện tích nhỏ nhất bằng

A.  1 4

B.  1 2

C.  3 4

D.  3 2

#Mẫu giáo
1
CM
Cao Minh Tâm
4 tháng 1 2018

Đúng(0)
PT
Pham Trong Bach
14 tháng 1 2017
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x  0 < x < α . Mặt phẳng  α  qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất. A.  x ...
Đọc tiếp

Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x  0 < x < α . Mặt phẳng  α  qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.

A.  x = a 4

B. x = a 3

C.  x = a 2

D.   x = a 5

#Mẫu giáo
1
CM
Cao Minh Tâm
14 tháng 1 2017

Đáp án đúng : C

Đúng(0)
PT
Pham Trong Bach
4 tháng 5 2019
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x (0<x<a). Mặt phẳng  ( α )  qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất. A.  x = a 4 B. x = ...
Đọc tiếp

Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x (0<x<a). Mặt phẳng  ( α )  qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.

A.  x = a 4

B. x = a 3

C. x = a 2

D. x = a 5

#Mẫu giáo
1
CM
Cao Minh Tâm
4 tháng 5 2019

Đáp án đúng : C

Đúng(0)
PT
Pham Trong Bach
15 tháng 2 2019
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, tam giác SAB đều. Gọi M là điểm trên cạnh AD sao cho A M = x ;   x ∈ 0 ; a . Mặt phẳng α  đi qua M và song song với (SAB) lần lượt cắt các cạnh CB, CS, SD tại N, P, Q. Tìm x để diện tích tứ giác MNPQ bằng  ...
Đọc tiếp

Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, tam giác SAB đều. Gọi M là điểm trên cạnh AD sao cho A M = x ;   x ∈ 0 ; a . Mặt phẳng α  đi qua M và song song với (SAB) lần lượt cắt các cạnh CB, CS, SD tại N, P, Q. Tìm x để diện tích tứ giác MNPQ bằng  2 a 2 3 9

A.  2 a 3

B.  a 4

C.  a 2

D.  a 3

#Mẫu giáo
1
CM
Cao Minh Tâm
15 tháng 2 2019

Đáp án là D

Đúng(0)
PT
Pham Trong Bach
13 tháng 6 2017
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = 1, AC = 2; cạnh bên SA vuông góc với đáy và SA = 1. Gọi I là trung điểm của AC. Xét M là điểm thay đổi trên cạnh AB sao cho A M = x 0 < x < 1  và (P) là mặt phẳng đi qua M, song song với SA và IB. Thiết diện của hình chóp với mặt...
Đọc tiếp

Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = 1, AC = 2; cạnh bên SA vuông góc với đáy và SA = 1. Gọi I là trung điểm của AC. Xét M là điểm thay đổi trên cạnh AB sao cho A M = x 0 < x < 1  và (P) là mặt phẳng đi qua M, song song với SA và IB. Thiết diện của hình chóp với mặt phẳng (P) có diện tích lớn nhất thì giá trị của x bằng.

A.  2 3

B.  3 4

C.  1 3

D.  1 2

#Mẫu giáo
1
CM
Cao Minh Tâm
13 tháng 6 2017

Chọn A

Đúng(0)
PT
Pham Trong Bach
18 tháng 10 2017
Cho tứ diện ABCD. Gọi I là trung điểm của BC, M là điểm trên cạnh DC. Một mp α  qua M, song song BC và AI. Gọi P, Q lần lượt là giao điểm của  α  với BD và AD. Xét các mệnh đề sau: (1) MP // BC                   (2) MQ // AC                  (3) PQ // AI                     (4) (MPQ) // (ABC) Số mệnh đề đúng là: A. 1 B. 3 C. 2 ...
Đọc tiếp

Cho tứ diện ABCD. Gọi I là trung điểm của BC, M là điểm trên cạnh DC. Một mp α  qua M, song song BC và AI. Gọi P, Q lần lượt là giao điểm của  α  với BD và AD. Xét các mệnh đề sau:

(1) MP // BC                   (2) MQ // AC                  (3) PQ // AI                     (4) (MPQ) // (ABC)

Số mệnh đề đúng là:

A. 1

B. 3

C. 2

D. 4
#Mẫu giáo
1
CM
Cao Minh Tâm
18 tháng 10 2017

Chọn B.

 Phương pháp:

+) Với (P), (Q), (R) là 3 mặt phẳng phân biệt, có 

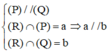
+) Chứng minh hai mặt phẳng song song:

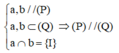
Cách giải:

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP