Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có:
C n 8 = 26 C n 4 ⇔ n ! 8 ! n − 8 ! = 26 n ! 4 ! n − 4 ⇔ n − 7 n − 6 n − 5 n − 4 = 13 .14.15.16 ⇔ n − 7 = 13 ⇔ n = 20
Số tập con gồm k phần tử của A là: C 20 k ⇒ k = 10 thì C 20 k nhỏ nhất.

Đáp án D
Số tập con của A có 8 phần tử C n 8 và số tập của A có 4 phần tử là C n 4
⇒ 26 = C n 8 C n 4 = 4 ! n − 4 ! 8 ! n − 8 ! = n − 7 n − 5 n − 4 1680 ⇔ n = 20.
Số tập con gồm k phần tử là C 20 k .
Khi xảy ra
C 20 k > C 20 k + 1 ⇔ 20 ! k ! 20 − k ! > 20 ! k + 1 ! 19 − k ! ⇔ k + 1 > 20 − k ⇔ k > 9 , 5
Vậy với thì đạt giá trị nhỏ nhất

C n 1 ; C n 2 ; C n 3 lần lượt là số các tập con của A gồm 1;3;5… phần tử. Ta luôn có
C n 0 + C n 1 + . . + C n n = 2 n ⇒ C n 0 + C n 1 + . . . = 2 n - 1
Từ giả thiết ta có phương trình:
2 n - 1 = 16 n ⇔ 2 n - 5 = n
Vì n > 4 nên ta xét n = 5 thấy không thỏa (*), do đó ta xét
n
≥
6
;
n
∈
ℤ
Xét hàm số f x = 2 x - 5 - x liên tục trên nửa khoảng [ 6 ; + ∞ ) , x ∈ ℤ .
Ta có f ' x = 2 x - 5 ln 2 - 1 > 0 ; ∀ x ≥ 6 ⇒ f x liên tục và đồng biến trên nửa khoảng [ 6 ; + ∞ ) , x ∈ ℤ và f(8) = 0 nên x = 8 là nghiệm duy nhất của phương trình. 2 x - 5 - x = 0 ; x ≥ 6 . Vậy n = 8 thỏa mãn đề bài.
Đáp án A

Đáp án A
Số tập con gồm 2 phần tử của tập hợp n phần tử là C n 2 = 45 ⇒ n = 10

Ta có :
\(K=\frac{2\sqrt{x}+3}{\sqrt{x}-5}=\frac{2\sqrt{x}-10}{\sqrt{x}-5}+\frac{13}{\sqrt{x}-5}=2+\frac{13}{\sqrt{x}-5}\)là số nguyên dương
<=> 13 chia hết cho \(\sqrt{x}-5\)
<=> \(\sqrt{x}-5\inƯ\left(13\right)=\left\{-13;-1;1;13\right\}\)
<=> \(\sqrt{x}\in\left\{-12;4;6;18\right\}\)
<=> \(x\in\left\{16;36;324\right\}\) (vì \(\sqrt{x}\ge0\))
Do x nguyên và x có GTLN nên x = 324

Đáp án C
Điều kiện: n≥7
Số tập con có 7 phân tử và 3 phân tử của A là C n 7 và C n 3
Suy ra
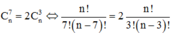
![]()



