Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
🕘. Giờ đầu tiên, chú sâu đi 1 mét, giờ thứ hai đi hai mét, ... Cuối mỗi giờ, chú sâu quay trái hoặc phải một góc bằng 90 độ. Hỏi vào lúc 4 giờ chiều, khoảng cách tối thiểu giữa chú sâu và tổ là bao nhiêu mét?
Có ΔABC cân ở A
=> AB = AC
H là trung điểm BC
=> HB = HC
Xét Δ AHB và ΔAHC có :
AB = AC ( cmt )
HB = HC ( cmt )
AH chung
=> ΔAHB = ΔAHC ( c.c.c)
Xét tam giác ABH và tam giác AHC
Ta có AB=AC( tam giác ABC cân tại A)
AH là cạnh chung
BH=HC(gt)
Do đó tam giác ABH= tam giác ACH(c.c.c)
suy ra BAH=HAC(2 góc tương ứng)
hay BAM=CAM
Xét tam giác ABM và tam giác AMC
Ta có AB=AC(cmt)
AM là cạnh chung
BAM=CAM(cmt)
Do đó tam giác ABM=tam giác ACM( c.g.c)
suy ra BM=MC( 2 cạnh tương ứng)
suy ra tam giác MBC cân tại M
Lại có ANB=MBC(AN song song với BC)
Mà MBC=MBA( BM là tia phân giác của ABC)
Nên ANB=MBA( =MBC)
suy ra tam giác ABN cân tại A
suy ra AB=AN( tính chất)
Ta có a.(a+b+c)+b.(a+b+c)+c.(a+b+c)=1/144
=>ta sử dụng phép phân phối có a+b+c chung
=>(a+b+c)(a+b+c)=1/144
=>a+b+c=1/12
từ đó tính a,b,c lần lượt là -1/2;3/4;-1/6
cậu toàn chép sai đề bài à nếu là c.(a+b+c)=-1/72 mới tính được
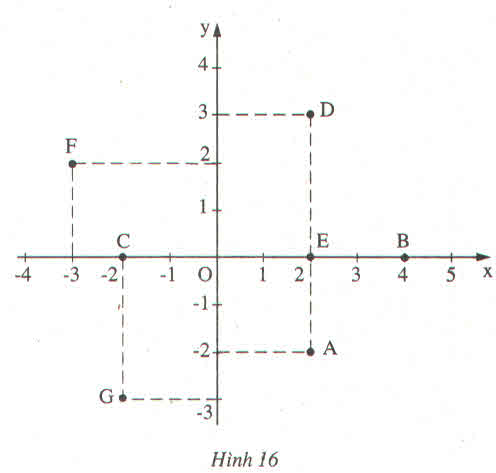
a) Tọa độ các điểm trong hình vẽ là:
A(2;-2); B(4;0); C(-2;0); D(2;3); E(2;0);F(-3;2); G(-2;-3)
b) Ta có hình vẽ ∆ABC:
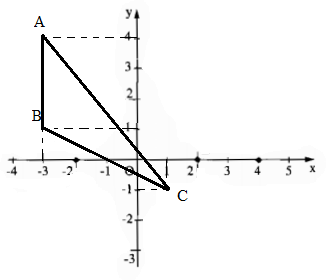
A(-3;4); B(-3;1); C(1;-1).
Mình giúp bạn nha
Ta có : \(3m+4n-mn=16\)
\(\Rightarrow m\left(3-n\right)+4n-12=4\)
\(\Rightarrow m\left(3-n\right)-4\left(3-n\right)=4\)
\(\Rightarrow\left(m-4\right)\left(3-n\right)=4\)
\(\Rightarrow\) \(\left[{}\begin{matrix}m-4\in\left\{1,2,4,-1,-2,-4\right\}\\3-n\in\left\{4,2,1,-4,-2,-1\right\}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}m\in\left\{5,6,8,3,2,0\right\}\\n\in\left\{-1,1,2,7,5,4\right\}\end{matrix}\right.\)
đoạn cuối khi tìm m,n bạn kẻ bảng cho dễ làm (trong này không có kẻ nên mình làm tạm vậy nha )
a) \(VT=\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=3\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^8-1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^{16}-1\right)\left(2^{16}+1\right)=2^{32}-1=VP\)
Vậy \(\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)=2^{32}-1\)
a: Trực tâm là điểm D
b: EF=căn 3^2+4^2=5cm
c: DF=căn 10^2-6^2=8cm