Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) bc=a2 suy ra 2RsinB.2RsinC=(2RsinA)2=4RsinA2
suy ra sinB.sinC=sinA2
còn cái còn lại bạn dựa vào công thức tính diên tích nhé
chứng minh ha2=hb.hc
ta có S=\(\dfrac{1}{2}a.h_a=\dfrac{1}{2}bh_b=\dfrac{1}{2}ch_c\)
suy ra : 2S=a.ha=bhb=chc
suy ra : a2ha2=b.c.hb.hc mà a2=b.c
suy ra : ha2=hb.hc

Số phần tử của tập hợp A = { k2 + 1 | k εℤ, |k| \(\le\)2} là:
A. 1
B. 2
C. 3
D. 5

a: góc C=90-30=60 độ
Xét ΔBAC vuông tại A có cos B=AB/BC
nên \(BC=\dfrac{2\sqrt{3}}{cos30}=4\left(cm\right)\)
=>AC=2cm
b: Xét ΔbAC vuông tại A có cos B=AB/BC
nên AB/BC=1/2
=>BC=2
=>AC=căn 3

Bài 1:
Áp dụng BĐT Bunhiacopxky ta có:
\((a^2+2c^2)(1+2)\geq (a+2c)^2\)
\(\Rightarrow \sqrt{a^2+2c^2}\geq \frac{a+2c}{\sqrt{3}}\)
\(\Rightarrow \frac{\sqrt{a^2+2c^2}}{ac}\geq \frac{a+2c}{\sqrt{3}ac}=\frac{ab+2bc}{\sqrt{3}abc}\)
Hoàn toàn tương tự: \(\left\{\begin{matrix} \frac{\sqrt{c^2+2b^2}}{bc}\geq \frac{ac+2ab}{\sqrt{3}abc}\\ \frac{\sqrt{b^2+2a^2}}{ab}\geq \frac{bc+2ac}{\sqrt{3}abc}\end{matrix}\right.\)
Cộng theo vế các BĐT trên thu được:
\(\text{VT}\geq \frac{1}{\sqrt{3}}.\frac{ab+2bc+ac+2ab+bc+2ac}{abc}=\frac{1}{\sqrt{3}}.\frac{3(ab+bc+ac)}{abc}=\frac{1}{\sqrt{3}}.\frac{3abc}{abc}=\sqrt{3}\)
Ta có đpcm
Dấu bằng xảy ra khi $a=b=c=3$
Bài 2: Bài này sử dụng pp xác định điểm rơi thôi.
Áp dụng BĐT AM-GM ta có:
\(24a^2+24.(\frac{31}{261})^2\geq 2\sqrt{24^2.(\frac{31}{261})^2a^2}=\frac{496}{87}a\)
\(b^2+(\frac{248}{87})^2\geq 2\sqrt{(\frac{248}{87})^2.b^2}=\frac{496}{87}b\)
\(93c^2+93.(\frac{8}{261})^2\geq 2\sqrt{93^2.(\frac{8}{261})^2c^2}=\frac{496}{87}c\)
Cộng theo vế:
\(B+\frac{248}{29}\geq \frac{496}{87}(a+b+c)=\frac{496}{87}.3=\frac{496}{29}\)
\(\Rightarrow B\geq \frac{496}{29}-\frac{248}{29}=\frac{248}{29}\)
Vậy \(B_{\min}=\frac{248}{29}\). Dấu bằng xảy ra khi: \((a,b,c)=(\frac{31}{261}; \frac{248}{87}; \frac{8}{261})\)
Chọn C.
Vì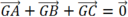 nên
nên
Gọi M, N, P lần lượt là trung điểm của BC, CA, AB
Tam giác ABM đều nên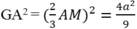
Theo định lý Pitago ta có:
Suy ra