Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

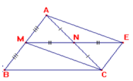
a) ta có : AM=MB(gt)
AN=NC(gt)
suy ra ; MN là đường trung bình của ▲ABC
→MN//BC→MNBC là hình thang
b) tứ giác AECM có;
AB=BC(N trung điểm)
MN=NE(gt)
→AECM là hình bình hành

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
hay BMNC là hình thang

A M N E B C
\(a)\)Xét \(\Delta ABC\)ta có :
\(\hept{\begin{cases}AM=MB\\AN=NC\end{cases}\Rightarrow}MN\text{ là đường trung bình của}\Delta ABC\)
=> MN // BC
=> BMNC là hình thang
\(b)\text{Xét tứ giác }AECM\text{ có }:\)
\(\hept{\begin{cases}AN=NC(N\text{ là trung điểm của AC})\\MN=NE(E\text{ đối xứng với M qua N})\end{cases}}\Rightarrow AECM\text{ là hình bình hành}\)
Tự làm câu c đi bạn

a: Xét ΔBAC có AM/AB=AN/AC
nên MN//BC và MN=1/2BC
=>BMNC là hình thang
b: Xét tứ giác AECM có
N là trung điểm chung của AC và EM
nên AECM là hình bình hành

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
hay BMNC là hình thang
b: Xét tứ giác AMCE có
N là trung điểm của AC
N là trung điểm của ME
Do đó: AMCE là hình bình hành
c: Để AECM là hình chữ nhật thì CM⊥AM
=>ΔCAB cân tại C
Để AECM là hình thoi thì CM=MA
=>CM=AB/2
=>ΔCBA vuông tại C