Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(tự vẽ hình )
câu 4:
a) có AB2 + AC2 = 225
BC2 = 225
Pytago đảo => \(\Delta ABC\)vuông tại A
b) Xét \(\Delta MAB\)và \(\Delta MDC\)
MA = MD (gt)
BM = BC ( do M là trung điểm của BC )
\(\widehat{AMB}=\widehat{CMD}\)( hai góc đối đỉnh )
=> \(\Delta MAB\)= \(\Delta MDC\) (cgc)
c) vì \(\Delta MAB\)= \(\Delta MDC\)
=> \(\hept{\begin{cases}AB=DC\\\widehat{MAB}=\widehat{MDC}\end{cases}}\)
=> AB// DC
lại có AB \(\perp\)AC => DC \(\perp\)AC => \(\Delta KCD\)vuông tại C
Xét \(\Delta\) vuông ABK và \(\Delta\)vuông KCD:
AB =CD (cmt)
AK = KC ( do k là trung điểm của AC )
=> \(\Delta\)vuông AKB = \(\Delta\)vuông CKD (cc)
=> KB = KD
d. do KB = KD => \(\Delta KBD\)cân tại K
=> \(\widehat{KBD}=\widehat{KDB}\)(1)
có \(\Delta ADC\)vuông tại C => \(AD=\sqrt{AC^2+DC^2}=15\)
=> MD = 7.5
mà MB = 7.5
=> MB = MD
=> \(\Delta MBD\)cân tại M
=> \(\widehat{MBD}=\widehat{MDB}\)(2)
Từ (1) và (2) => \(\widehat{KBD}-\widehat{MBD}=\widehat{KDB}-\widehat{MDB}\)hay \(\widehat{KBM}=\widehat{KDM}\)
Xét \(\Delta KBI\)và \(\Delta KDN\)có:
\(\widehat{KBI}=\widehat{KDN}\)(cmt)
\(\widehat{KBD}\)chung
KD =KB (cmt)
=> \(\Delta KBI\)= \(\Delta KDN\)(gcg)
=> KN =KI
=. đpcm
câu 5:
a) Xét \(\Delta ABM\)và \(\Delta MDC\):
MA=MD(gt)
MB=MC (M là trung điểm của BC)
\(\widehat{BMA}=\widehat{DMC}\)( đối đỉnh )
=> \(\Delta BMA=\Delta CMD\)(cgc)
b) Xét \(\Delta\)vuông ABC
có AM là đường trung tuyến của tam giác
=> \(AM=\frac{1}{2}BC\)mà \(BM=MC=\frac{1}{2}BC\)(do M là trung điểm của BC )
=> AM = BM = MC
có MA =MD => AM = MD =MB =MC
=> BM +MC = AM +MD hay BC =AD
Xét \(\Delta BAC\)và \(\Delta DCA\)
AB =DC
AC chung
BC =DC
=> \(\Delta BAC\)= \(\Delta DCA\)(ccc)
c. Xét \(\Delta ABM\)
BM=AM
\(\widehat{ABM}\)= 600
=> đpcm

A B C M N O H K 1 2 1 2
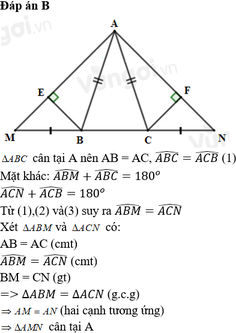
Cm: a) Ta có: góc ABC + góc ABM = 1800 (kề bù)
góc ACN + góc ACB = 1800 (kề bù)
và góc ABC = góc ACB (vì t/giác ABC cân tạo A)
=> góc ABM = góc ACN
Xét t/giác ABM và t/giác ACN
có AB = AC (gt)
góc ABM = góc ACN (cmt)
BM = CN (gt)
=> t/giác ABM = t/giác ACN (c.g.c)
b) ko đề
c) Xét t/giác AHB và t/giác AKC
có góc H1 = góc K1 = 900 (gt)
AB = AC (gt)
góc HAB = góc KAC (vì t/giác ABM = t/giác ACN)
=> t/giác AHB = t/giác AKC (ch - gn)
=> AH = AK (hai cạnh tương ứng)
Xét t/giác AHO và t/giác AKO
có AH = AK (cmt)
góc H1 = góc K1 = 900 (gt)
AO : chung
=> t/giác AHO = t/giác AKO (ch - cgv)
=> HO = KO(hai cạnh tương ứng)
Mà HB + BO = HO
KC + CO = OK
và HB = KC (vì t/giác AHB = t/giác AKC)
=> BO = CO
=> t/giác OBC là t/giác cân tại O

Hình bạn tự vẽ nha :))
a)* Ta có: \(\Delta ABC\)cân tại A <=> AB=AC
\(\hept{\begin{cases}AM=AB+MB\\AN=AC+NC\end{cases}\Rightarrow AM=AN}\)(do \(AB=AC;MB=NC\))
\(\Rightarrow\Delta AMN\)cân tại A
* Từ \(\Delta ABC\)cân tại A, có: \(\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\)(1)
Từ \(\Delta AMN\)cân tại A, có: \(\widehat{AMN}=\frac{180^o-\widehat{A}}{2}\)(2)
Từ (1) và (2), suy ra: \(\widehat{ABC}=\widehat{AMN}\)
\(\Rightarrow MN//BC\)(2 góc đồng vị bằng nhau)
b) Xét \(\Delta ABI\)và \(\Delta ACI\)có:
\(\hept{\begin{cases}AB=AC\\AIchung\\IB=IC\end{cases}\Rightarrow\Delta ABI=\Delta}ACI\left(ccc\right)\)
\(\Rightarrow\widehat{BAI}=\widehat{CAI}\)(2 góc tương ứng)
\(\Rightarrow AI\)là p/giác của \(B\widehat{A}C\) (3)
Tương tự, ta có: \(\widehat{MAE}=\widehat{NAE}\)
\(\Rightarrow AE\)là p/ giác của \(\widehat{BAC}\)(4)
Từ (3) và (4), ta có: A,I,E thẳng hàng

a)\(\widehat{C}=\widehat{BAH}=90^O-\widehat{CAH}\)
\(\widehat{B}=\widehat{CAH}=90^O-\widehat{BAH}\)
b)Ta có:
\(\widehat{ADC}=\widehat{B}+\widehat{BAD}=\widehat{B}+\frac{\widehat{BAH}}{2}=\widehat{B}+\widehat{\frac{C}{2}}\)
Lại có:
\(\widehat{DAC}=180^O-\widehat{C}-\widehat{ADC}=180^O-\widehat{C}-\left(\widehat{B}+\widehat{\frac{C}{2}}\right)=\left(90^O-\widehat{B}\right)-\frac{\widehat{C}}{2}+\left(90^O-\widehat{C}\right)\)
\(=\widehat{C}-\widehat{\frac{C}{2}}+\widehat{B}=\widehat{B}+\frac{\widehat{C}}{2}\)
Suy ra:\(\widehat{ADC}=\widehat{DAC}\)
\(\Rightarrow\Delta ADC\)cân tại C
c)\(DK\perp BC;AH\perp BC\Rightarrow DK//AH\)
\(\Rightarrow\widehat{KDA}=\widehat{DAH}\)(hai góc so le trong)
Mà \(\widehat{BAD}=\widehat{DAH}\)
\(\Rightarrow\widehat{BAD}=\widehat{KDA}\)
\(\Rightarrow\)\(\Delta KAD\)cân tại K
d)Xét \(\Delta CDK-\Delta CAK\)
\(\hept{\begin{cases}CD=CA\\KD=KA\\CA.chung\end{cases}}\)
\(\Rightarrow\Delta CDK=\Delta CAK\left(c.c.c\right)\)
\(\Rightarrowđpcm\)
e)Xét\(\Delta AID-\Delta AHD\)
\(\hept{\begin{cases}AI=AH\\AD.chung\\\widehat{DAI}=\widehat{DAH}\end{cases}}\)
\(\Rightarrow\widehat{AID}=\widehat{AHD}=90^O\)
\(\Rightarrow DI\perp AB.Mà.AC\perp AB\)
\(\Rightarrow DI//AC\)

Bài làm
Vì ΔABCΔABC cân nên ⇒Bˆ=C1ˆ⇒B^=C1^
Mà C1ˆ=C2ˆC1^=C2^ ( 2 góc đối đỉnh ) ⇒Bˆ=C2ˆ⇒B^=C2^
Xét ΔABDΔABD vàΔICEΔICE có
CI=CA(gt)Bˆ=Cˆ2BD=CE(gt)⇒ΔABD=ΔICE(c−g−c)CI=CA(gt)B^=C^2BD=CE(gt)⇒ΔABD=ΔICE(c−g−c)
2) Xét ΔBMDΔBMD và ΔNECΔNEC có:
BMDˆ=CNEˆ=(900)Bˆ=C2ˆ(cmt)BD=CE⇒ΔBMD=ΔNECBMD^=CNE^=(900)B^=C2^(cmt)BD=CE⇒ΔBMD=ΔNEC ( cạnh huyền - góc nhọn)
⇒BM=CN⇒BM=CN ( 2 cạnh tương ứng )
~Học tốt!~