Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

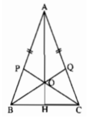
a: Xét ΔPBC và ΔQCB có
PB=QC
\(\widehat{PBC}=\widehat{QCB}\)
BC chung
Do đo: ΔPBC=ΔQCB
Suy ra: \(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
b: OB=OC
AB=AC
Do đó: AO là đường trung trực của BC
Ta có: ΔABC cân tại A
mà AO là đường trung trực
nên AO là đường phân giác
hay O cách đều hai cạnh AB và AC

Ta sẽ chứng minh ΔOBC có hai góc OBC và OCB bằng nhau
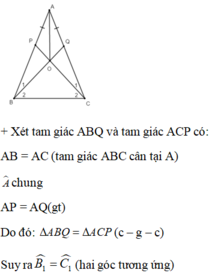
ΔABQ và ΔACP có: AB = AC, AQ = AP, ∠A chung
⇒ ΔABQ = ΔACP (c.g.c)
⇒ ∠ABQ = ∠ACP.
Mà ∠ABC = ∠ACB (Vì tam giác ABC cân tại A)
⇒ ∠ABC - ∠ABQ = ∠ACB - ∠ACP hay ∠OBC = ∠OCB
⇒ ΔOBC cân tại O.

ΔOBC cân tại O ⇒ OB = OC.
ΔAOB và ΔAOC có: AO chung, AB = AC (giả thiết), OB = OC (cmt)
⇒ ΔAOB = ΔAOC (c.c.c).
⇒ ∠BAO = ∠CAO
⇒ AO là tia phân giác của góc BAC
⇒ O cách đều hai cạnh AB, AC

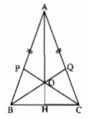
a) Xét tam giác ACP và tam giác ABQ
có: AC= AB (gt)
góc A là góc chung
AP =AQ (gt)
\(\Rightarrow\Delta ACP=\Delta ABQ\left(c-g-c\right)\)
\(\Rightarrow\widehat{ACP}=\widehat{ABQ}\) ( 2 góc tương ứng)
mà góc ACP + góc PCB = góc ACB
góc ABQ + góc QBC = góc ABC
mà góc ACB = góc ABC (gt)
=> góc ACP + góc PCB = góc ABQ + góc QBC
=> góc PCB = góc QBC
=> tam giác OBC cân tại O ( định lí tam giác cân)
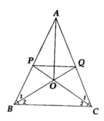
b) ( kẻ OM vuông góc với AB tại M, ON vuông góc với AC tại N)
ta có: tam giác OBC cân tại O ( phần a)
=> OB =OC ( định lí )
xét tam giác OMB vuông tại M và tam giác ONC vuông tại N
có: góc ABQ = góc ACP ( phần a)
OB =OC (gt)
=> tam giác OMB = tam giác ONC ( cạnh góc vuông- góc nhọn)
c) ta có: tam giác OMB = tam giác ONC ( phần b)
=> OM = ON ( 2 cạnh tương ứng)
Xét tam giác OAM vuông tại M và tam giác OAN vuông tại N
có: OM =ON ( cmt)
OA là cạnh chung
=> tam giác OAM = tam giác OAN ( cạnh góc vuông- cạnh huyền)
=> góc OAM = góc OAN ( 2 góc tương ứng)
Xét tam giác BADvà tam giác CAD
có: BA =CA (gt)
góc OAM = góc OAN ( cmt)
AD là cạnh chung
=> tam giác BAD = tam giác CAD ( c-g-c)
=> BD = CD ( 2 cạnh tương ứng) (1)
góc BDA = góc CDA ( 2 góc tương ứng)
mà góc BDA + góc CDA = 180 độ ( kề bù)
\(\Rightarrow\widehat{BDA}=\widehat{CDA}=\frac{180^0}{2}=90^0\)
=> góc BDA = góc CDA = 90 độ
=> AD vuông góc với BC tại E (2)
từ (1); (2) => AD là đường trung trực của BC ( định lí)
k cho mk nha!!!

Câu 1:
Xét tam giác AMB và tam giác AMC ta có:
AB = AC (tam giác ABC cân tại A)
ABM = ACM (tam giác ABC cân tại A)
=> Tam giác AMB = tam giác AMC (ch-gn) (dpcm)
Câu 2:
a) Ta có: +) AK+KB = AB => KB = AB-AK
+) AH+HC = AC => HC = AC-AH
Mà AB=AC(tam giác ABC cân tại A) ; AK=AH (gt)
=>KB=HC
Xét tam giác BHC và tam giác CKB ta có:
HC=KB (cmt)
HCB=KBC (tam giác ABC cân tại A)
BC là cạnh chung
=>tam giác BHC = tam giác CKB (c.g.c)
=>BH=CK (2 cạnh tương ứng) (dpcm)
Xét tam giác ABH và tam giác ACK ta có:
AB=AC (tam giác ABC cân tại A)
BH=CK (cmt)
AH=AK (gt)
=> tam giác ABH = tam giác ACK (c.c.c)
=> ABH = ACK (2 góc tương ứng) (dpcm)
b) Theo a) tam giác BHC= tam giác CKB
=> HBC=KCB (2 góc tương ứng) hay OBC=OCB
=> Tam giác OBC là tam giác cân tại O (dpcm)
c) Theo b tam giác OBC cân tại O => OB=OC
Theo a góc ABH = góc ACK => KBO= HCO
Xét tam giác OKB và tam giác OHC ta có:
KB=HC (theo a)
KBO=HCO (cmt)
OB=OC (cmt)
=> tam giác OKB = tam giác OHC (c.g.c)
=> OK = OH (2 cạnh tương ứng) hay tam giác OKH là tam giác cân tại O (dpcm)
d) Gọi giao điểm của AO và KH là I
Xét tam giác AKO và tam giác AHO ta có:
AK=AH (gt)
AO là cạnh chung
OK=OH (theo c)
=> tam giác AKO = tam giác AHO (c.c.c)
=> KAO = HAO (2 góc tương ứng) hay KAI=HAI
Xét tam giác KAI và tam giác HAI ta có:
AK=AH (gt)
KAI=HAI (cmt)
AI là cạnh chung
=> tam giác KAI = tam giác HAI ( c.g.c)
=> KI=HI , mà I nằm giữa H và K
=> I là trung điểm của KH hay
AO đi qua trung điểm của KH (dpcm)