
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



A K M I C H B N
a)
Ta có nối K với M
=> Xét t/gMCK và t/gMHC ta có:
CK=CH (gt) hay ^KCM=^MCH (gt)
MC (cạnh chung)
=>t/gMCK = t/gMCH (c.g.c)
=>MK=MH ( tương ứng)
đpcm.
b) Tiếp tục nối K và H
Gọi I là giao điểm của CM và KH
Xét t/gICK và t/gICH ta có:
CK=CH (gt) hay ^HCM=^CMK (gt)
CI (cạnh chung)
=>t/gICK=t/gICH (c.g.c)
=>^CIK=^CIH( tương ứng)
Mà ^CIK+^CIH=180o( góc kề bù)
=>^CIK=^CIH=90o
=>CI_|_HK
=>CM_|_HK
đpcm.
c) Quan sát hình ta thấy ^CMH=65o=^CMN=65o (1)
Vì ^KCM+^MCN=90o
=>^MCN=90o-^KCM
=>^MCN=90o-35o
=>^MCN=65o(2)
Từ (1) và (2) vì ^NMC=^NCM => t/gNMC là t/g cân.
đpcm.

a)\(\widehat{C}=\widehat{BAH}=90^O-\widehat{CAH}\)
\(\widehat{B}=\widehat{CAH}=90^O-\widehat{BAH}\)
b)Ta có:
\(\widehat{ADC}=\widehat{B}+\widehat{BAD}=\widehat{B}+\frac{\widehat{BAH}}{2}=\widehat{B}+\widehat{\frac{C}{2}}\)
Lại có:
\(\widehat{DAC}=180^O-\widehat{C}-\widehat{ADC}=180^O-\widehat{C}-\left(\widehat{B}+\widehat{\frac{C}{2}}\right)=\left(90^O-\widehat{B}\right)-\frac{\widehat{C}}{2}+\left(90^O-\widehat{C}\right)\)
\(=\widehat{C}-\widehat{\frac{C}{2}}+\widehat{B}=\widehat{B}+\frac{\widehat{C}}{2}\)
Suy ra:\(\widehat{ADC}=\widehat{DAC}\)
\(\Rightarrow\Delta ADC\)cân tại C
c)\(DK\perp BC;AH\perp BC\Rightarrow DK//AH\)
\(\Rightarrow\widehat{KDA}=\widehat{DAH}\)(hai góc so le trong)
Mà \(\widehat{BAD}=\widehat{DAH}\)
\(\Rightarrow\widehat{BAD}=\widehat{KDA}\)
\(\Rightarrow\)\(\Delta KAD\)cân tại K
d)Xét \(\Delta CDK-\Delta CAK\)
\(\hept{\begin{cases}CD=CA\\KD=KA\\CA.chung\end{cases}}\)
\(\Rightarrow\Delta CDK=\Delta CAK\left(c.c.c\right)\)
\(\Rightarrowđpcm\)
e)Xét\(\Delta AID-\Delta AHD\)
\(\hept{\begin{cases}AI=AH\\AD.chung\\\widehat{DAI}=\widehat{DAH}\end{cases}}\)
\(\Rightarrow\widehat{AID}=\widehat{AHD}=90^O\)
\(\Rightarrow DI\perp AB.Mà.AC\perp AB\)
\(\Rightarrow DI//AC\)

A B C H
Cm: Xét t/giác ABH và t/giác ACH
có góc B = góc C (vì t/giác ABC cân tại A)
AB = AC (gt)
góc AHB = góc AHC = 900 (gt)
=> t/giác ABH = t/giác ACH (ch - gn)
=> HB = HC (hai cạnh tương ứng)
=> góc BAH = góc CAH (hai góc tương ứng)
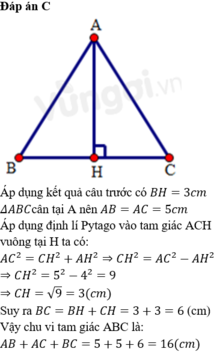
b) Ta có: HB = HC = AB/2 = 8/2 = 4 (cm)
Áp dụng định lí Py - ta - go vào t/giác ABH vuông tại H, ta có:
AB2 = HB2 + AH2
=> AH2 = 52 - 42 = 25 - 16 = 9
=> AH = 3
Vậy AH = 3 cm
c) Xem lại đề

https://h.vn/hoi-dap/question/38145.html
bạn xem ở đây nhé
a) Ta có: tam giác ABC cân tại A nên đường cao AH còn là đường trung tuyến
Suy ra: H là trung điểm của BC
BH = BC/2 = 3cm
Áp dụng định lý Py ta go ta có: AH = căn (AB^2 - BH^2) = 4cm
b)Ta có: G là trọng tâm của tam giác ABC nên G thuộc giao của ba đường trung tuyến của tam giác
Suy ra: G thuộc đường trung tuyến kẻ từ A
Mà ở câu a, AH còn là đường trung tuyến nên G thuộc AH
Vậy: A,G,H thẳng hàng
c)Tam giác ABC cân tại A, có AH là đường cao nên còn là đường phân giác
Suy ra: góc BAG = góc CAG
Xét tam giác ABG và tam giác ACG có:
AB = AC (tam giác ABC cân tại A)
góc BAG = góc CAG (cm trên)
AG chung
Vậy tam giác ABG = tam giác ACG (c-g-c)
Suy ra: góc ABG = góc ACG

A B C M H K P Q D E x y
a) Xét \(\Delta\)AMC và \(\Delta\)AHB có: ^ACM = ^ABH (=450); AC=AB; ^MAC = ^BAH (Cùng phụ ^BAM)
=> \(\Delta\)AMC = \(\Delta\)AHB (g.c.g) => AM=AH (2 cạnh tương ứng). Tương tự: AM=AK
=> AH=AK=AM. Hay AH=AK=1/2.HK (đpcm)
b) Gọi D và E lần lượt là hình chiếu của A trên MH và MK.
Xét \(\Delta\)HMK: MA trung tuyến (Do DH=AK), MA=AH=AK; MA vuông góc HK
=> \(\Delta\)HMK vuông cân tại M => ^HMK = 900 ; MA là phân giác ^HMK.
Xét ^HMK: MA là tia phân giác; AD và AE vuông góc MH; MK => AD=AE
Dễ thấy: ^DAE = 900 (Vì ^ADM = ^AEM = ^EMD = 900) => ^DAP = ^EAQ (Cùng phụ ^DAQ)
Xét \(\Delta\)ADP và \(\Delta\)AEQ có: ^ADP = ^AEQ (=900); AD=AE; ^DAP = ^EAQ (cmt)
=> \(\Delta\)ADP = \(\Delta\)AEQ (g.c.g) => AP=AQ (2 cạnh tương ứng).
Từ đó: \(\Delta\)PAQ vuông cân tại A. Dễ dàng chỉ ra PQ // BC (đpcm).
Cách 2: chứng minh phần b:
Xét tg HMK
có: HA = AK ( chứng minh phần a); \(MA\perp HK⋮A\)(gt)
=> tg HMK cân tại M ( định lí)
=> HM = MK (t/c)
Xét tg ABM và tg ACK
có: AB = AC(gt); ^ABM = ^ACK ( dễ chứng minh ^ABM = ^ACK = 45 độ); ^BAM = ^CAK ( khi cộng với ^MAC đều = 90 độ)
=> tg ABM = tg ACK ( c-g-c)
=> BM = CK ( 2 cạnh t/ ư)
Xét tg BMH vuông tại B và tg CKM vuông tại C
có: BM = CK (cmt); MH = KM (cmt)
=> tg BMH = tg CKM ( cgv-ch)
=> ^BHP = ^ CMQ ( 2 góc t/ ư)
HB = MC ( 2 cạnh t/ ư)
Xét tg HBP và tg MCQ
có: ^HBP = ^ MCQ ( dễ chứng minh ^HBP = ^MCQ = 45 độ); HB = MC (cmt); ^BHP = ^CMQ (cmt)
=> tg HBP = tg MCQ ( g-c-g)
=> BP = CQ ( 2 cạnh t/ ư)
=> AP = AQ ( = AB- BP = AC - CQ)
và ^PAQ = 90 độ (gt)
=> tg PAQ vuông cân tại A ( định lí)
=> ^APQ = 45 độ
=> ^APQ = ^CBP ( = 45 độ)
mà ^APQ và ^CBP đồng vị
=> PQ // BC ( định lí)
...
xl bn! bn theo cách bn kia vẫn đúng đó, mk chỉ thêm 1 cách nữa thôi!

ta có:tam giác ABC vuông tại A=> góc B+góc C=900
mà A=2B,A=900=>B=450
=>C=450 hay tam giác ABC vuông cân tại A=>AB=AC
áp dụng đ/l PyTaGo ta có:
BC2=AB2+AC2
mà AB=AC(cmt)
=>BC2=\(\left(2\sqrt{2}\right)^2+\left(2\sqrt{2}\right)^2=16\)
=>BC=4cm