Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.Xét tam giác vuông AHB và tam giác vuông AHC, có:
AB = AC ( ABC cân )
góc B = góc C ( ABC cân )
Vậy tam giác vuông AHB = tam giác vuông AHC ( cạnh huyền. góc nhọn)
=> HB = HC ( 2 cạnh tương ứng )
b.Xét tam giác vuông ADH và tam giác vuông AEH, có:
AH: cạnh chung
góc DAH = góc EAH ( AH là đường cao cũng là đường phân giác )
Vậy tam giác vuông ADH = tam giác vuông AEH
=> HD = HE ( 2 cạnh tương ứng )
=> tam giác HDE cân tại H
c.Xét tam giác vuông AEC và tam giác vuông ADB, có:
AB = AC ( ABC cân )
góc A: chung
Vậy tam giác vuông AEC = tam giác vuông ADB ( cạnh huyền.góc nhọn)
=> AD = AE ( 2 cạnh tương ứng )
=> tam giác ADE cân tại A
=> AH vuông với DE, mà AH cũng vuông với BC
=> DE//BC ( DE ko phải DC nha bạn )
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó:ΔAHB=ΔAHC
Suy ra: HB=HC
b: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: HD=HE
hay ΔHDE cân tại H
c: Ta có: ΔADH=ΔAEH
nên AD=AE
Xét ΔABC có AD/AB=AE/AC
nên DE//BC

Em tham khảo lời giải tại đây nhé.
Câu hỏi của Acot gamer - Toán lớp 7 - Học toán với OnlineMath

A B C H
a/ Xét tam giác AHB và tam giác AHC
Góc AHB=AHC=90 độ
AB=AC(tam giác ABC cân tại A)
Góc B=C (tam giác ABC cân tại A)
=> Tam giác ABH=ACH(ch-gn)
mk nha

Bài 1 xét hai tam giác AHB và tam giác AHC có:
AC= AB (cân)
AH là cạnh chung
góc ABH= gó ACH
=> hai tam giác bằng nhau theo trường hợp cạnh huyền góc nhọn
bài 2
a) ta có tam giác ABC cân
và AH là đường cao => AH cũng là đường trung tuyến của tam giác ABC
hoặc dùng kết quả 2 tam giác bằng nhau ở câu 1 để suy ra cũng dc
b)từ kết quả baì 1 suy ra hai góc bằng nhau
ta có tam giác ABH vuông tại H
HB=HC+1/2BC=5
sử dụng pytago
AH2 = AB2- BH2

A B C M N Q P O R S T A B C H M D I A B C D K G M K E P F (Hình a) (Hình b) (Hình c) Q I
Bài toán 1: (Hình a)
Gọi đường thẳng qua N vuông góc với AN cắt AC tại R, qua P kẻ đường thẳng song song với BC. Đường thẳng này cắt AM,AN,BC lần lượt tại S,T,K.
Ta thấy \(\Delta\)APR có AN vừa là đường cao, đường phân giác => \(\Delta\)APR cân tại A => AP = AR, NP = NR
Áp dụng hệ quả ĐL Thales \(\frac{BM}{PS}=\frac{CM}{KS}\left(=\frac{AM}{AS}\right)\)=> PS = KS
Áp dụng ĐL đường phân giác trong tam giác: \(\frac{TK}{TP}=\frac{AK}{AP}\Rightarrow\frac{ST+SK}{TP}=\frac{AK}{AR}\)
\(\Rightarrow\frac{2ST+PT}{TP}=\frac{AR+RK}{AR}\Rightarrow\frac{2ST}{TP}=\frac{RK}{AR}\)
Dễ thấy NS là đường trung bình của \(\Delta\)RKP => RK = 2NS. Do đó \(\frac{ST}{TP}=\frac{NS}{AR}\)
Đồng thời NS // AR, suy ra \(\frac{ST}{TP}=\frac{NS}{AR}=\frac{SQ}{QA}\)=> QT // AP (ĐL Thaels đảo)
Mà AP vuông góc PO nên QT vuông góc PO. Từ đây suy ra T là trực tâm của \(\Delta\)POQ
=> QO vuông góc PT. Lại có PT // BC nên QO vuông góc BC (đpcm).
Bài toán 2: (Hình b)
Ta có IB = IC => \(\Delta\)BIC cân tại I => ^IBC = ^ICB = ^ACB/2 => \(\Delta\)MCI ~ \(\Delta\)MBC (g.g)
=> MC2 = MI.MB. Xét \(\Delta\)AHC có ^AHC = 900 , trung tuyến HM => HM = MC
Do đó MH2 = MI.MB => \(\Delta\)MIH ~ \(\Delta\)MHB (c.g.c) => ^MHI = ^MBH = ^MBC = ^MCI
=> Tứ giác CHIM nội tiếp. Mà CI là phân giác ^MCH nên (IH = (IM hay IM = IH (đpcm).
Bài toán 3: (Hình c)
a) Gọi đường thẳng qua C vuông góc CB cắt MK tại F, DE cắt BC tại Q, CG cắt BD tại I.
Áp dụng ĐL Melelaus:\(\frac{MB}{MC}.\frac{GA}{GB}.\frac{DC}{DA}=1\)suy ra \(\frac{DC}{DA}=2\)=> A là trung điểm DC
Khi đó G là trọng tâm của \(\Delta\)BCD. Do CG cắt BD tại I nên I là trung điểm BD
Dễ thấy \(\Delta\)BCD vuông cân tại B => BI = CM (=BC/2). Từ đó \(\Delta\)IBC = \(\Delta\)MCF (g.c.g)
=> CB = CF => \(\Delta\)BCF vuông cân ở C => ^CBA = ^CBF (=450) => B,A,F thẳng hàng
=> CA vuông góc GF. Từ đó K là trực tâm của \(\Delta\)CGF => GK vuông góc CF => GK // CM
Theo bổ đề hình thang thì P,Q lần lượt là trung điểm GK,CM. Kết hợp \(\Delta\)CEM vuông ở E
=> EQ=CM/2. Áp dụng ĐL Melelaus có \(\frac{GD}{GM}.\frac{EQ}{ED}.\frac{CM}{CQ}=1\)=> \(\frac{EQ}{ED}=\frac{1}{4}\)
=> \(\frac{ED}{CM}=2\)=> DE = 2CM = BC (đpcm).
b) Theo câu a thì EQ là trung tuyến của \(\Delta\)CEM vuông tại E => EQ = QC => ^QEC = ^QCE
Vì vậy ^PEG = ^QEC = ^QCE = ^PGE => \(\Delta\)EPG cân tại P => PG = PE (đpcm).

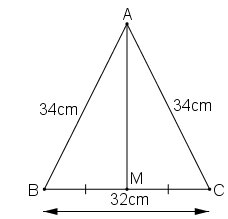
a. Xét ΔAMB và ΔAMC, ta có:
AM = AC (gt)
BM = CM (gt)
AM cạnh chung
Suy ra: ΔAMB = ΔAMC (c.c.c)
Suy ra: ∠(AMB) = ∠(AMC) (1)
Lại có: ∠(AMB) + ∠(AMC) = 180o (hai góc kề bù) (2)
Từ (1) và (2) suy ra: ∠(AMB) = ∠(AMC) = 90o
Vậy AM ⊥ BC.
b. Tam giác AMB có ∠(AMB) = 90o
Áp dụng định lí Pi-ta-go vào tam giác vuông AMB, ta có:
AB2 = AM2 + BM2 ⇒ AM2 = AB2 - BM2 = 342 - 162
= 1156 - 256 = 900
Suy ra: AM = 30 (cm).

Đề có 2 chỗ sai:
Thứ nhất: phân giác trong của góc ABC không thể cắt AB tại D, phải là cắt BC tại D.
Thứ hai: tam giác ABC cân tại A nên:
* AB = AC
* đường phân giác AD cũng chính là đường cao => AD vuông góc BC
tam giác ADC vuông tại D nên: AD2 + DC2 = AC2
mà AB = AC => AD2 + DC2 = AB2

theo dề bài ta có
AH Là dường cao của tam giác ABC
=>tam giác AHB và tam giác AHC vuông tại H
Xét tam giác ABC cân tại A ta có
AH Là dường cao kẻ từ dỉnh A
=>AH cũng là dường trung tuyến ứng cạnh BC
=> BH=HC
xét tam giác AHB (góc H =90 dộ )và tam giác AHC (góc H =90 dộ )
AB=AC(do tam giác ABC cân tại A
BH=HC(chứng minh trên)
=>tam giác AHB=tam giác AHC (cạnh huyền- cạnh góc vuông)
C2
theo dề bài ta có
AH vuông góc vs BC
=>Ah là dường cao cua tam giác ABc
=>tam giác AHB và tam giác AHc vuông tại h
xét tam giác AHB (H =90 độ)và tam giác AHC (h=90 dộ )
AH là cạnh chung
BH=HC(chứng minh như trên )
=>Tam giác AHB=tam giác AHC (hai cạnh góc vuông )

theo đề bài ta có
AH Là dường cao của tam giác ABC
=>tam giác AHB và tam giác AHC vuông tại H
Xét tam giác ABC cân tại A ta có
AH Là dường cao kẻ từ dỉnh A
=>AH cũng là dường trung tuyến ứng cạnh BC
=> BH=HC
xét tam giác AHB (góc H =90 dộ )và tam giác AHC (góc H =90 dộ )
AB=AC(do tam giác ABC cân tại A
BH=HC(chứng minh trên)
=>tam giác AHB=tam giác AHC (cạnh huyền- cạnh góc vuông)
C2 theo dề bài ta có
AH vuông góc vs BC
=>Ah là dường cao cua tam giác ABc
=>tam giác AHB và tam giác AHc vuông tại h
xét tam giác AHB (H =90 độ)và tam giác AHC (h=90 dộ )
AH là cạnh chung
BH=HC(chứng minh như trên )
=>Tam giác AHB=tam giác AHC (hai cạnh góc vuông )
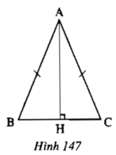
- Cách 1: ΔABC cân tại A nên ∠B = ∠C và AB = AC
Xét hai tam giác vuông ΔAHB và ΔAHC đều vuông tại H có:
AB = AC (GT)
∠B = ∠C
⇒ ΔAHB =ΔAHC (cạnh huyền – góc nhọn)
- Cách 2:
Xét hai tam giác vuông ΔAHB và ΔAHC đều vuông tại H có:
AB = AC
AH chung
⇒ ΔAHB = ΔAHC (cạnh huyền – cạnh góc vuông)