Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x=A\sin(\omega t)+A\cos(\omega t)\)
\(=A\sin(\omega t)+A\sin(\omega t+\dfrac{\pi}{2})\)
\(=2A\sin(\omega t+\dfrac{\pi}{4}).\cos \dfrac{\pi}{4}\)
\(=A\sqrt 2\sin(\omega t+\dfrac{\pi}{4})\)
Vậy biên độ dao động là: \(A\sqrt 2\)
Chọn C.

Áp dụng công thức (5.1 và 5.2 - SGK) ta tìm được:
A = 2,3 cm và φ = 0,73π
Phương trình dao động tổng hợp là: x = 2,3cos(5πt + 0,73π) (cm).

Sử sụng hệ thức: 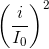 +
+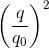 = 1
= 1
Thay số và giải hệ phương trình trìm I0 và q0
Tần số góc: ω = 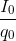 = 50 (rad/s)
= 50 (rad/s)

Ta có $x_1=x_{12}-x_2=x_{12}-(x_{23}-(x_{13}-x_1)$
$\Rightarrow$ $2x_1=x_{12}-x_{23}+x_{13}$. Bấm máy tính ta được
${x_1}={3\sqrt{6}}\cos\left({\pi t + \dfrac{\pi}{12}} \right)$
${x_3}={3\sqrt{2}}\cos\left({\pi t + \dfrac{7\pi}{12}} \right)$
Suy ra hai dao động vuông pha, như vậy khi x1 đạt giá trị cực đại thì x3 bằng 0.
![]()
cách bấm máy để ra phương trình dao động làm như thế nào vậy ạ

Hướng dẫn bạn:
- Lực kéo về: \(F=k.x=0,03\sqrt 2\pi\) (không biết có đúng như giả thiết của bạn không)
\(\Rightarrow x =\dfrac{0,03\sqrt 2\pi}{k}=\dfrac{0,03\sqrt 2\pi}{m.\omega^2}=\dfrac{0,03\sqrt 2\pi}{0,01.\omega^2}=\dfrac{3\sqrt 2\pi}{\omega^2}\)
- Áp dụng: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow 0,05^2=(\dfrac{3\sqrt 2\pi}{\omega^2})^2+\dfrac{(0,4\pi)^2}{\omega^2}\)
Bạn giải pt trên tìm \(\omega \) và suy ra chu kì \(T\) nhé.

Bạn đổi ra cùng hàm cos rồi lấy máy tính mà bấm cho nhanh :)
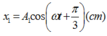
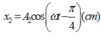


 D
D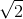
Đáp án B
Phương pháp: Sử dụng giản đồ vecto và định lí hàm số sin trong tam giác
Cách giải:
- Phương trình dao động của x; x1; x2: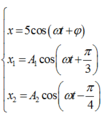
Suy ra :
+ Độ lệch pha giữa x và x1 là :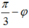
+ Độ lệch pha giữa x và x2 là :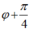
+ Độ lệch pha giữa x1 và x2 là :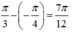
=> Ta có giản đồ vecto :
- Áp dụng định lí hàm số sin trong tam giác ta có:
có: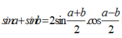
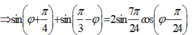
Để [A1 + A2] đạt cực đại thì