Đề thi HSG quận Đống Đa - Hà Nội vòng 2 ( một trong 2 đề khó nhất chỉ sau quận Cầu Giấy )
Câu 1:(5đ)
1. Cho \(a,b,c\) là số thực thỏa mãn:
\(ab+bc+ca=2015\). Tính giá trị biểu thức:
\(P=\frac{a}{2015+a^2}+\frac{b}{2015+b^2}+\frac{c}{2015+c^2}-\frac{4030}{2015\left(a+b+c\right)-abc}\)
2. Cho \(a,b,c\) là các số nguyên thỏa mãn:
\(a^3+b^3=5c^3\)
CMR: \(a+b+c\) chia hết cho \(6\)
3. Tìm các cặp \(\left(x;y\right)\) nguyên thỏa mãn:
\(x^2\left(y^2+1\right)+y^2+24=12xy\)
Câu 2:(5đ)
a) \(3x+\sqrt{5-x}=2\sqrt{x-3}+11\)
b) \(2x^2+4x-8=\left(2x+3\right)\sqrt{x^2-3}\)
Câu 3:(2đ)
Cho các số thực \(x,y\) thỏa mãn điều kiện:
\(x-\sqrt{x+1}=\sqrt{y+5}-y\)
Tìm GTLN của \(P=x+y\)
Câu 4:(6đ)
Qua \(M\) cố định ở ngoài đường tròn \(\left(O;R\right)\). Qua \(M\) kẻ các tiếp tuyến \(MA,MB\) ( \(A,B\) là các tiếp tuyến ). Qua \(P\) di động trên cung nhỏ \(AB\) ( \(P\) khác \(A;B\) ) dựng tiếp tuyến của \(\left(O\right)\) cắt \(MA,MB\) lần lượt tại \(E\) và \(F\).
a) CMR: Chu vi tam giác \(MEF\) không đổi khi \(P\) di động trên \(AB\).
b) Lấy \(N\) trên tiếp tuyến \(MA\) sao cho \(N,F\) khác phía \(AB\) và \(AN=BF\). CMR: \(AB\) đi qua trung điểm của \(NF\).
c) Kẻ đường thẳng \(d\) qua \(M\) của \(\left(O\right)\) tại \(H\) và \(K\). Xác định vị trí của \(d\) để \(MH+HK\) đạt GTNN
Câu 5:(2đ)
1. Cho \(p\)là số nguyên tố thỏa mãn \(p^2+2018\) là số nguyên tố. CMR: \(6p^2+2015\) là số nguyên tố.
2. Cho tập \(x=\left\{1;2;3...;2015\right\}\). Tô màu các phần tử \(x\)bởi \(5\) màu: xanh, đỏ, vàng, tím, nâu. CMR tồn tại \(3\) phần tử \(a,b,c\) của \(x\)sao cho \(a\) là bội của \(b\); \(b\)là bội của \(c\)


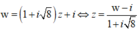
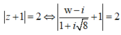
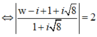
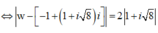
![]()





Đáp án C