Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

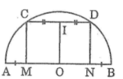
Ta có: MC // ND (gt)
Suy ra tứ giác MCDN là hình thang
Lại có: OM + AM = ON + BN (= R)
Mà AM = BN (gt)
Suy ra: OM = ON
Kẻ OI ⊥ CD (3)
Suy ra: IC = ID (đường kính dây cung)
Khi đó OI là đường trung bình của hình thang ACDN
Suy ra: OI // MC // ND (4)
Từ (3) và (4) suy ra: MC ⊥ CD, ND ⊥ CD.

a) Xét tứ giác AOMC có
ˆCAOCAO^ và ˆCMOCMO^ là hai góc đối
ˆCAO+ˆCMO=1800(900+900=1800)CAO^+CMO^=1800(900+900=1800)
Do đó: AOMC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Ta có: AOMC là tứ giác nội tiếp(cmt)
nên ˆMAO=ˆOCMMAO^=OCM^(hai góc cùng nhìn cạnh OM)
hay ˆMAB=ˆOCDMAB^=OCD^
Xét (O) có
CM là tiếp tuyến có M là tiếp điểm(Gt)
CA là tiếp tuyến có A là tiếp điểm(Gt)
Do đó: OC là tia phân giác của ˆAOMAOM^(Tính chất hai tiếp tuyến cắt nhau)
⇔ˆAOM=2⋅ˆCOM⇔AOM^=2⋅COM^
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm(gt)
DB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: OD là tia phân giác của ˆMOBMOB^(Tính chất hai tiếp tuyến cắt nhau)
⇔ˆBOM=2⋅ˆMOD⇔BOM^=2⋅MOD^
Ta có: ˆAOM+ˆBOM=1800AOM^+BOM^=1800(hai góc kề bù)
mà ˆAOM=2⋅ˆCOMAOM^=2⋅COM^(cmt)
và ˆBOM=2⋅ˆMODBOM^=2⋅MOD^(cmt)
nên 2⋅ˆCOM+2⋅ˆMOD=18002⋅COM^+2⋅MOD^=1800
⇔ˆCOM+ˆMOD=900⇔COM^+MOD^=900
mà ˆCOM+ˆMOD=ˆCODCOM^+MOD^=COD^(tia OM nằm giữa hai tia OC,OD)
nên ˆCOD=900COD^=900
Xét ΔCOD có ˆCOD=900COD^=900(cmt)
nên ΔCOD vuông tại O(Định nghĩa tam giác vuông)
Xét (O) có
ΔMAB nội tiếp đường tròn(M,A,B∈(O))
AB là đường kính(gt)
Do đó: ΔMAB vuông tại M(Định lí)
Xét ΔAMB vuông tại M và ΔCOD vuông tại O có
ˆMAB=ˆOCDMAB^=OCD^(cmt)
Do đó: ΔAMB∼ΔCOD(g-g)
⇔AMCO=BMDOAMCO=BMDO(Các cặp cạnh tương ứng tỉ lệ)
hay AM⋅OD=BM⋅OCAM⋅OD=BM⋅OC(đpcm)



Ta có: CM ⊥ CD
DN ⊥ CD
Suy ra: CM // DN
Kẻ OI ⊥ CD
Suy ra: OI // CM // DN
Ta có: IC = ID (đường kính dây cung)
Suy ra: OM = ON (1)
Mà: AM + OM = ON + BN (= R) (2)
Từ (1) và (2) suy ra: AM = BN