Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Đổi 0,1mm2 = 1. 10-7 m2 . Áp dụng công thức tính điện trở \(R=\rho\frac{l}{S}\) ; thay số và tính \(\Rightarrow\) RAB = 6W
b/ Khi \(AC=\frac{BC}{2}\) \(\Rightarrow\) RAC = \(\frac{1}{3}\).RAB Þ RAC = 2W và có RCB = RAB - RAC = 4W
Xét mạch cầu MN ta có \(\frac{R_1}{R_{AC}}=\frac{R_2}{R_{CB}}=\frac{3}{2}\) nên mạch cầu là cân bằng. Vậy IA = 0
c/ Đặt RAC = x ( ĐK : \(0\le x\le6\Omega\) ) ta có RCB = ( 6 - x )
* Điện trở mạch ngoài gồm ( R1 // RAC ) nối tiếp ( R2 // RCB ) là \(R=\frac{3.x}{3+x}+\frac{6.\left(6-x\right)}{6+\left(6-x\right)}=\)= ?
* Cường độ dòng điện trong mạch chính : \(I=\frac{U}{R}\) ?
* Áp dụng công thức tính HĐT của mạch // có : UAD = RAD . I = \(\frac{3.x}{3+x}.I=\) ?
Và UDB = RDB . I = \(\frac{6.\left(6-x\right)}{12-x}I\) = ?
* Ta có cường độ dòng điện qua R1 ; R2 lần lượt là : I1 = \(\frac{U_{AD}}{R_1}\) = ? và I2 = \(\frac{U_{DB}}{R_2}\) = ?
+ Nếu cực dương của ampe kế gắn vào D thì : I1 = Ia + I2 Þ Ia = I1 - I2 = ? (1)
Thay Ia = 1/3A vào (1) Þ Phương trình bậc 2 theo x, giải PT này được x = 3W ( loại giá trị -18)
+ Nếu cực dương của ampe kế gắn vào C thì : Ia = I2 - I1 = ? (2)
Thay Ia = 1/3A vào (2) Þ Phương trình bậc 2 khác theo x, giải PT này được x = 1,2W ( loại 25,8 vì > 6 )
* Để định vị trí điểm C ta lập tỉ số \(\frac{AC}{CB}=\frac{R_{AC}}{R_{CB}}\) = ? \(\Rightarrow\) AC = 0,3m

a) Rtd= \(\frac{1}{R_1}+\frac{1}{R_2}\)= \(\frac{1}{15}+\frac{1}{10}\)=6 \(\Omega\)
b) I=\(\frac{U}{R}\)(định luật ôm)=\(\frac{18}{6}\)=3(A)

- Bước 1: Mắc mạch điện như hình vẽ
R0 Rb A K2 K1
|
||
|
- Bước 2: Chỉ đóng khóa K1, số chỉ của ampe kế là I1. Ta có: U = I1(RA + R0) (1)
|
||
|
- Bước 3: Chỉ đóng K2 và dịch chuyển con chạy để ampe kế chỉ vẫn I1. Khi đó phần biến trở tham gia vào mạch điện có giá trị bằng Rb = R0. |
||
|
- Bước 4: Giữ nguyên vị trí con chạy của biến trở ở bước 3 rồi đóng cả K1 và K2, số chỉ ampe kế là I2. Ta có: U = I2(RA + R0/2) (2)
|
||
|
- Giải hệ phương trình (1) và (2) ta tìm được: \(R_A=\dfrac{\left(2I_1-I_2\right)R_0}{2\left(I_2-I_1\right)}\) . |

a) Vì R1 nt R2 nên: Rtd = R1 + R2= 24+12= 36(ôm)
R1 nt R2 thì: I= I1= I2 = 0,5 (A)
HĐT giữa 2 đầu mỗi điện trờ là: I1=U1/R1 => U1=I1.R1 = 0,5 x 24= 12 (V)
I2=U2/R2 => U2=I2.R2= 0,5 x 12= 6(V)
b) Đổi: 20p = 1200s
Nhiệt lượng toả ra trong 20p của đoạn mạch là: Q= I2.Rtd.t= (0,5)2 . 36.1200= 10800(J)
c) Tóm tắt:
R3//R1
I2=3I1
Giải:

Tóm tắt
R1 = R2= R3 = R4 = 2Ω
R5 = 4Ω ; R6 = R8 =3Ω
R7 = R9 = 1Ω
RA = 0
---------------------------------------
a) RAB = ?
b) UAB = 12V
I1, I2, I3, I4, I5, I6, I7, I8, I9 = ?
IA1, IA2, IA3 = ? Giải a) Do điện trở các ampe kế không đáng kể nên ta chập các điểm C, D, E, B. Ta có sơ đồ tương đương. Cấu trúc mạch:
\(< \left|\left\{\left[\left(R_4ntR_3\right)\text{//}\left(R_9ntR_8\right)\right]ntR_2\right\}\text{//}\left(R_7ntR_6\right)\right|ntR_1>\text{//}R_5\)
Ta có:
\(R_{34}=R_3+R_4=2+2=4\left(\Omega\right)\\ R_{89}=R_8+R_9=3+1=4\left(\Omega\right)\\ \Rightarrow R_{HB}=\dfrac{R_{34}.R_{89}}{R_{34}+R_{89}}=\dfrac{4.4}{4+4}=2\left(\Omega\right)\\ \Rightarrow R_{2HB}=R_2+R_{HB}=2+2=4\left(\Omega\right)\\ R_{67}=R_6+R_7=3+1=4\left(\Omega\right)\\ \Rightarrow R_{FB}=\dfrac{R_{67}.R_{2HB}}{R_{67}+R_{2HB}}=\dfrac{4.4}{4+4}=2\left(\Omega\right)\\ \Rightarrow R_{1FB}=R_1+R_{FB}=R_1+R_{FB}=2+2=4\left(\Omega\right)\\ \Rightarrow R_{AB}=\dfrac{R_5.R_{1FB}}{R_5+R_{1FB}}=\dfrac{3.4}{3+4}=\dfrac{12}{7}\left(\Omega\right)\)
Cấu trúc mạch:
\(< \left|\left\{\left[\left(R_4ntR_3\right)\text{//}\left(R_9ntR_8\right)\right]ntR_2\right\}\text{//}\left(R_7ntR_6\right)\right|ntR_1>\text{//}R_5\)
Ta có:
\(R_{34}=R_3+R_4=2+2=4\left(\Omega\right)\\ R_{89}=R_8+R_9=3+1=4\left(\Omega\right)\\ \Rightarrow R_{HB}=\dfrac{R_{34}.R_{89}}{R_{34}+R_{89}}=\dfrac{4.4}{4+4}=2\left(\Omega\right)\\ \Rightarrow R_{2HB}=R_2+R_{HB}=2+2=4\left(\Omega\right)\\ R_{67}=R_6+R_7=3+1=4\left(\Omega\right)\\ \Rightarrow R_{FB}=\dfrac{R_{67}.R_{2HB}}{R_{67}+R_{2HB}}=\dfrac{4.4}{4+4}=2\left(\Omega\right)\\ \Rightarrow R_{1FB}=R_1+R_{FB}=R_1+R_{FB}=2+2=4\left(\Omega\right)\\ \Rightarrow R_{AB}=\dfrac{R_5.R_{1FB}}{R_5+R_{1FB}}=\dfrac{3.4}{3+4}=\dfrac{12}{7}\left(\Omega\right)\)
mình sửa lại cái RAB của bài này nha
RAB= \(\dfrac{R5.R1FB}{R5+R1FB}\)=\(\dfrac{4.4}{4+4}\)=2\(\Omega\)
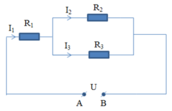



Ta thấy I1 = I23= 0,4A
Điện trở tương đương của đoạn mạch AB là:
Hiệu điện thế của mạch là:
Cường độ dòng điện qua điện trở R2: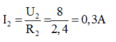
Cường độ dòng điện qua điện trở R3: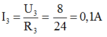
→ Đáp án D