Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
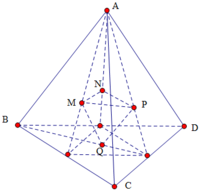
Vé hình ta thấy khối tứ diện MNPQ đồng dạng với tứ diệnABCD theo tỷ số k = 1 3
Do đó V M N P Q V A B C D = 1 3 3 = 1 27

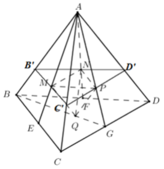
Ta có:
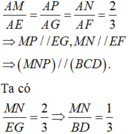
Ta có ∆ M N P đồng dạng với ∆ B C D theo tỉ số
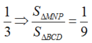
Dựng B ' C ' qua M và song song BC. C ' D ' qua P và song song với CD.
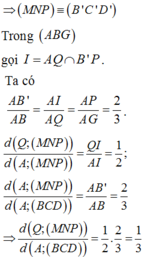

Chọn D.

Đáp án A
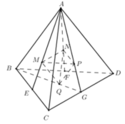
Giả sử tứ diện ABCD có AB;AC'AD đội một vuông góc ⇒ V A B C D = A B . A C . A D 6
Khi đó tứ diện MNPQ có MN;MP;MQ đội một vuông góc ⇒ V M . N P Q = M N . M P . M Q 6
Ta chứng minh được M N A B + M P A C + M Q A D = 1 ( dựa vào định lý Thalet), khi đó
M N . M P . M Q = A B . A C . A D . M N A B . M P A C . M Q A D ≤ A B . A C . A D . M N A B + M P A C + M Q A D 3 27 = A B . A C . A D 27
Vậy V M . N P Q = M N . M P . M Q 6 ≤ 1 27 . A B . A C . A D 6 = V 27 → V max = V 27

Đáp án A
Gọi M là trung điểm của AC và đặt độ dài AB = x
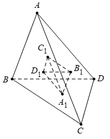
Vì B 1 , D 1 là trọng tâm tam giác A B C , A C D ⇒ M D 1 M B = M B 1 M D = 2 3
Suy ra:
B 1 D 1 / / B D ⇒ B 1 D 1 B D = M 1 D 1 M B = 1 3 ⇒ B 1 D 1 = B D 3
Tương tự, ta được A 1 B 1 C 1 D 1 là tứ diện đều cạnh x 3 ⇒ V V 1 = 27 ⇔ V 1 = V 3 3
Khi đó V 2 = V 1 3 3 = V 3 3.3 ; V 4 = V 3 3.4 → V n − V 3 3 n
Suy ra V + V 1 + ... + V n
= V 1 + 1 3 3 + 1 3 6 + 1 3 9 + ... + 1 3 3 n = V . S
Tống S là tổng của cấp số nhân với:
u 1 = 1 ; q = 1 27 ⇒ S = 1 − 1 27 1 − 1 27 n = 27. 1 − 27 − n 26
Vậy P = lim x → ∞ V .27 1 − 27 − n 26 = 27 26 V
vì lim x → + ∞ 27 − n = lim x → + ∞ 1 27 n = 0

Đáp án B
Ta có:
V M N P Q V A B C D = 1 3 . 1 3 2 = 1 27 ⇒ V M N P Q = V A B C D 27 = 9 3 27 = 3 3 c m 3

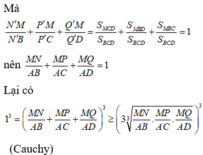

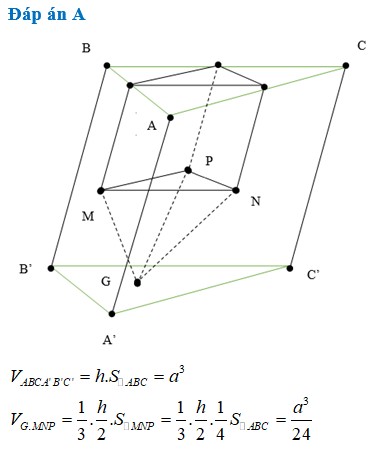

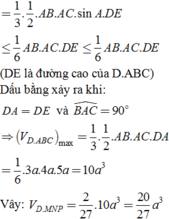
Đáp án là A
n