Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
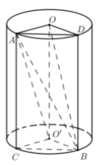
+ Gọi C là hình chiếu của A lên mặt đáy chứa đường tròn O ' ; R và D là hình chiếu của B lên mặt đáy chứa đường tròn (O;R).
+) Tính thể tích lăng trụ đứng O A D . O ' C B , từ đó suy ra thể tích tứ diện OO'AB và đánh giá.
Cách giải:

Chọn: D

Chọn đáp án C.
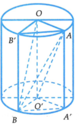
Kẻ các đường sinh AA', BB' của hình trụ (T).
Khi đó
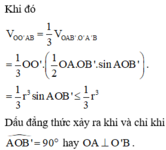
Như vậy, khối tứ diện có thể tích lớn nhất bằng
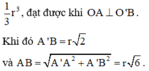

Xét đường thẳng ∆ đi qua điểm O và vuông gó với mặt phẳng (P). Gọi l là đưởng thẳng đi qua M0 ε (C) và l vuông góc với (P). Do đó l // ∆. Quay mặt phẳng (Q) tạo bởi l và ∆ quanh đường thẳng ∆, thì đường thẳng l vạch lên một mặt trụ tròn xoay. Mặt trụ này chứa tất cả những đường thẳng đi qua các điểm M ε (C) và vuông góc với (P). Trục của mặt trụ là ∆ và bán kính của trụ bằng r.

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

Đáp án D.
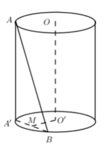
Phương pháp :
+) Xác định mặt phẳng (P) chứa AB và song song với OO’.
+) d(OO’;AB) = D(OO’;(P))
Cách giải :
Dựng AA’//OO’ ta có: (OO’;AB) = (AA’;AB) = A’AB = 300
Gọi M là trung điểm của A’B ta có:
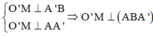
![]()
![]()
=>d(OO’;AB) = d(OO’;(ABA’)) = d(O’;(ABA’)) = O’M
Xét tam giác vuông ABA’ có ![]()
Xét tam giác vuông O’MB có 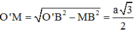

Đáp án C
Phương pháp:
+) Chứng minh mặt phẳng (P) không cắt đáy (O';R)
+) Tìm phần hình chiếu của mặt phẳng (P) trên mặt đáy. Tính S h c
+) Sử dụng công thức S h c = S . cos 60
Cách giải:
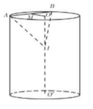
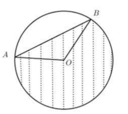
Gọi M là trung điểm của AB ta có:
O M = O A 2 − A B 2 2 = R 2 − 3 R 2 4 = R 2
Giả sử mặt phẳng (P) cắt trục OO’ tại I. Ta có : IA = IB nên Δ I A B cân tại I, do đó M I ⊥ A B


Vậy diện tích phần thiết diện cần tìm là :
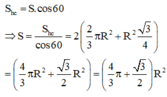

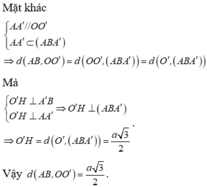
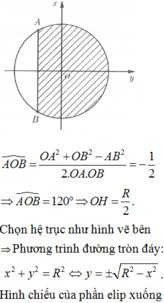

Đáp án A
Gọi P là hình chiếu của A trên đáy O ' . Khi đó
A B = A P 2 + P B 2 = h 2 + B P 2 = 4 R 2 + P B 2 ≤ 4 R 2 + 4 R 2 = 2 R 2
Dấu bằng xảy ra ⇔ B P = P Q = 2 R .