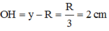Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Gọi I là tâm của hình tròn (C) và S là đỉnh của hình nón. Gọi bán kính của hình tròn (C) là r thì
![]()
Trường hợp 1: O nằm giữa S và I.
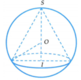
Chiều cao của hình chóp là SI = SO + OI = x + 6 (cm).
Thể tích khối chóp là V = 1 3 π 36 - x 2 x + 6 cm 3
Xét hàm số f x = 36 - x 2 x + 6 với 0 ≤ x < 6
Ta có f ' x = - 3 x 2 - 12 x + 36
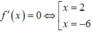
Do 0 ≤ x < 6 nên x = - 6.
Lập bảng biến thiên của hàm số ta thấy f(x) ta thấy f x ≤ f 2 = 256
Suy ra V ≤ V 1 = 1 3 π . 256 = 256 3 π cm 3
Dấu “=” xảy ra x = 2.
Trường hợp 2: I nằm giữa S và O
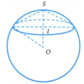
Chiều cao của hình chóp là SI = SO – OI = 6 – x (cm)
Thể tích của khối chóp là V = 1 3 π 36 - x 2 6 - x cm 3 (cm3).
Xét hàm số g x = 36 - x 2 6 - x với 0 ≤ x < 6
Ta có g ' x = 3 x 2 - 12 x - 36 < 0 , ∀ x ∈ 0 ; 6 nên hàm số g(x) nghịch biến trên 0 ; 6 .
Suy ra g x ≤ g 0 = 216
Khi đó V ≤ V 2 = 72 π cm 3 .
Dấu “=” xảy ra khi x = 0.
So sánh hai trường hợp 1 và 2, suy ra thể tích lớn nhất của khối chóp đã cho là V = 256 3 π cm 3 khi x = 2 c m .

Đáp án A.
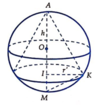
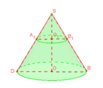
Kí hiệu như hình vẽ.
Ta thấy I K = r ' là bán kính đáy của hình chóp, A I = h là chiều cao của hình chóp.
Tam giác vuông tại K có IK là đường cao
⇒ I K 2 = A I . I M ⇒ r ' 2 = h . 2 r − h
Ta có V c o h p = 1 3 . π r ' 2 . h = 1 3 . π . h . h . 2 r − h = 4 3 π . h 2 . h 2 2 r − h .
Áp dụng bất đẳng thức Cauchy ta có
h 2 . h 2 . 2 r − h ≤ h 2 + h 2 + 2 r − h 3 27 = 8 r 3 27
⇔ V c h o p ≤ 4 3 π . 8 r 3 27 = 32 81 . π r 3
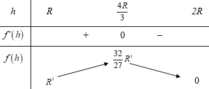
Dấu bằng xảy ra khi h 2 = 2 r − h ⇔ h = 4 r 3 . Vậy ta chọn A

Đáp án B
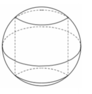
Gọi chiều cao và bán kính đáy của hình trụ nội tiếp mặt cầu lần lượt là h, r
Ta có tâm mặt cầu là trung tâm của đường nối 2 tâm các đường tròn đáy của hình trụ
Khi đó, bán kính mặt cầu ngoại tiếp khối trụ là R 2 = r 2 + h 2 4
Thể tích khối trụ là V = πr 2 h = π 4 4 R 2 - h 2 . h
Theo bất đẳng thức Cosi cho 3 số nguyên dương, ta có
4 R 2 - h 2 4 R 2 - h 2 2 h 2 ≤ 4 R 2 - h 2 + 4 R 2 - h 2 + 2 h 2 3 27
Nên 4 R 2 - h 2 . h 2 ≤ 256 R 6 27 ⇒ V ≤ π 4 4 R 2 - h 2 h ≤ 4 π 3 9 R 3
Dấu bằng xảy ra khi và chỉ khi 4 R 2 - h 2 = 2 h 2 ⇔ h = 2 R 3 3 .

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b
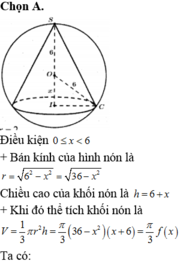
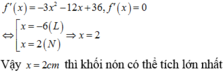
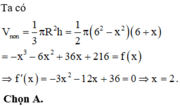

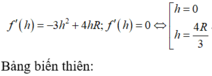
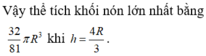


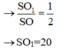
Đáp án A
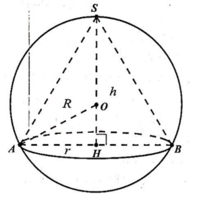
Kí hiệu bán kính đáy của hình nón là x, chiều cao hình nón là y (trong đó 0<x≤2R; 0<y≤R). Gọi SS’là đường kính của mặt cầu ngoại tiếp hình nón thì ta có:
Gọi V1 là thể tích khối nón: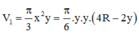
Mặt khác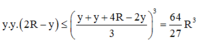
Do đó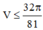 dấu bằng xảy ra
dấu bằng xảy ra 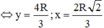
Khi đó