Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích hình vuông: 8.8 = 64(cm2)
Diện tích tam giác AED: 64.1/3 = 64/3(cm2)
Đặt EA = x, ta có: x.8.1/2 = 64/3 => x = 16/3(cm)
Vậy E thuộc AB sao cho AE = 16/3 cm

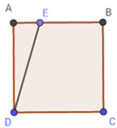
Gọi BE = x (m).
Diện tích hình vuông ABCD là: SABCD = AB2 = 102 = 100 (m2)
Diện tích hình thang vuông BCDE là:
SBCDE = ( B E + D C ) B C 2 = ( x + 10 ) .10 2 = 5 (x+10)
Vì diện tích hình thang vuông BCDE bằng 4 5 diện tích hình vuông ABCD nên ta có:
SBCDE = SABCD = 5(x + 10) = 4 5 .100 óx + 10 = 16 ó x = 6 (m)
Vậy điểm E ở trên cạnh AB sao cho BE = 6 m.
Đáp án cần chọn là: B

Ta có : \(S_{MNP}=S_{ABC}-S_{APC}-S_{CBM}-S_{ABN}\)
\(S_{APC}+S_{PEC}=S_{AEC}=\frac{1}{3}S_{ABC}\)
\(\Rightarrow S_{AEC}=\frac{1}{3}.126=42\left(cm^2\right)\)
Kẻ \(AH\perp CD,EK\perp CD\left(H,K\in CD\right)\)
Ta có : \(\frac{AH.DC}{2}==S_{ADC}=S_{BDC}=3.S_{DEC}=\frac{3}{2}.EK.DC\)
\(\Rightarrow AK=3EK\Rightarrow S_{ADC}=3S_{EPC}\)
\(\Rightarrow S_{EPC}=\frac{1}{4}S_{AEC}=\frac{1}{4}.42=10,5\left(cm^2\right)\)
\(\Rightarrow S_{APC}=42-10,5=31,5\left(cm^2\right)\)
Mà \(S_{CBM}=S_{BCD}-S_{BMD}\)
Tương tự
\(S_{BCD}=\frac{1}{2}.S_{ABC}=\frac{1}{2}.126=63\left(cm^2\right)\)
\(S_{BMC=54cm^2,}S_{ABN}=28cm^2\)
\(\Rightarrow S_{MNP}=126-31,5-54-28=12,5\left(cm^2\right)\)


Câu hỏi của Vũ Huy Hiệu - Toán lớp 9 - Học toán với OnlineMath
Em tham khảobài tương tự tại đây nhé.

Câu d, là câu riêng luôn rồi nhé
Đặt các cạnh hình vuông là a, BM= BE= x
\(\Rightarrow S_{MBE}=\frac{x^2}{2}\)
\(S_{AMD}=S_{CED}=\frac{a\left(a-x\right)}{2}\)
Ta có: \(S_{DEN}=a^2-\left(a\left(a-x\right)+\frac{x^2}{2}\right)\)
\(=\frac{2a^2-2a^2+2ax-x^2}{2}\)
\(=\frac{a^2-\left(a^2-2ax+x^2\right)}{2}\)
\(=\frac{a^2}{2}-\frac{\left(a-x\right)^2}{2}\le\frac{a^2}{2}\)
Dấu "=" xảy ra khi: a=x <=> BC=BE <=> E trùng C
Quá trình mình làm chỉ tắt những ý chính, bạn làm bài cần làm đầy đủ hơn!!!
Gọi BE = x (m).
Diện tích hình vuông ABCD là: SABCD = AB2 = 202 = 400 (m2)
Diện tích hình thang vuông BCDE là:
SBCDE = ( B E + D C ) B C 2 = ( x + 20 ) .20 2 = 10(x + 20)
Vì diện tích hình thang vuông BCDE bằng 3 4 diện tích hình vuông ABCD nên ta có:
SBCDE = 3 4 SABCD = 10(x + 20) = 3 4 .400 óx + 20 = 30 ó x = 10 (m)
Vậy điểm E ở trên cạnh AB sao cho BE = 10 m hay E là trung điểm đoạn AB.
Đáp án cần chọn là: D