Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
Chu vi hình tròn đáy : 2 x 5 x 3.14 = 31,4 ( cm )
Diện tích xung quanh hình trụ là :
31,4 x 12 = 376,8 ( cm2 )
Đ/s : 376, 8 cm2

Tham khảo tại đây nha:
Câu hỏi của Moe - Toán lớp 9 - Học toán với online math
mã câu :1308090

O O' A B H C F D K G E 1 2 3 4
a) Xét đường tròn (O';R) có: Đường kính OC và điểm A nằm trên cung OC => ^OAC=900
=> OA vuông góc với AC. Mà OA là bán kính của (O) => AC là tiếp tuyến của (O)
Ta thấy: 2 đường tròn (O) và (O') có cùng bán kính R => OA=OB=O'A=O'B= R
=> Tứ giác AOBO' là hình thoi =>OA // O'B
Lại có: OA vuông góc AC (cmt) => O'B vuông góc AC (Qhệ //, vg góc) hay BF vuông góc AC (đpcm).
b) Xét tứ giác ADKO: ^DKO=^OAD=900 (=^OAC)
=> Tứ giác ADKO nội tiếp đường tròn tâm là trg điểm OD (đpcm).
c) Do tứ giác AOBO' là hình thoi nên AB vuông góc OO' (tại H) (1)
Ta có điểm B thuộc (O') và F đối xứng B qua O' => F thuộc (O') (Vì đường tròn có tâm đối xứng)
Xét (O') đường kính BF và A thuộc cung BF => AB vuông góc AF (2)
Từ (1) và (2) => OO' // AF
Xét tứ giác AOO'F: OO' // AF; OA // O'F (cmt) => Tứ giác AOO'F là hình bình hành
=> AF = OO'. Mà AF=AD nên AD=OO'. Lại có: OO' = OA => AD=OA.
Xét tứ giác ADKO nội tiếp đường tròn => ^AOK+^ADK = 1800
Mà ^ADK + ^ADG = 1800 nên ^AOK=^ADG hay ^AOH=^ADG
Xét \(\Delta\)AHO và \(\Delta\)AGD: AO=AD (cmt); ^AOH=^ADG; ^AHO=^AGD=900
=> \(\Delta\)AHO=\(\Delta\)AGD (Cạnh huyền góc nhọn) => AH=AG
Xét tứ giác AHKG: ^AHK=^HKG=^HAG=900; AH=AG (cmt) => Tứ giác AHKG là hình vuông.
d) Dễ thấy: AO=OO'=O'A => Tam giác AOO' đều => ^AO'O = 600
Lại có: Hình bình hành AOO'F có O'O=O'F => Tứ giác AOO'F là hình thoi
=> ^AO'O=^AO'F = 600 => ^FO'C = 600
=> SHình quạt AO'O = 1/6 S (O) = \(\frac{R^2.\pi}{6}\)
Tương tự, suy ra: S H.quạt AO'O = S H.quạt BO'O = S H,quạt AOO' = S H.quạt BOO' = \(\frac{R^2.\pi}{6}\)
Cộng tất cả lại => \(S_1+S_2+S_3+S_4+2.S_{AOBO'}=4.\frac{R^2.\pi}{6}=\frac{2R^2.\pi}{3}\)
\(\Rightarrow S_1+S_2+S_3+S_4+S_{AOBO'}=\frac{2R^2.\pi}{3}-S_{AOBO'}\)
\(\Rightarrow S_{P.C}=\frac{2R^2.\pi}{3}-R^2.\frac{\sqrt{3}}{2}=\frac{4R^2.\pi}{6}-\frac{3\sqrt{3}.R^2}{6}=\frac{R^2.\left(4\pi-3\sqrt{3}\right)}{6}\)
\(=\frac{R^2.\left(4.3,14-3.1,73\right)}{6}=\frac{R^2.7,37}{6}\)(Chú thích SPhần chung: SP.C)
Vậy diện tích phần chung của (O0 và (O') tính theo R là \(S_{P.C}=\frac{7,37.R^2}{6}.\)
F G A B C E O' K D N O
a) Xét đường tâm O'
\(\widehat{OAC}=90^o\)

Theo đề bài ta có:
Diện tích hình chữ nhật ABCD là: AB.AD=2a\(^2\) (1)
Chu vi hình chữ nhật là: 2(AB+CD)=6a⇒AB+CD=3a ( 2 )
Từ (1) và (2), ta có ABAB và CDCD là nghiệm của phương trình:
x\(^2\)− 3ax − 2a\(^2\)=0
Giải phương trình ta được: x\(_1\)= 2a; x\(_2\)=a
Theo giả thiết AB>AD nên ta chọn AB=2a; AD=a
Khi quay hình chữ nhật quanh ABAB ta được hình trụ có h=AB=2a và r=AD=a
Vậy diện tích xung quanh hình trụ là:
Sxq=2π.AD.AB=2π.a.2a=4πa\(^2\)
Thể tích hình trụ là:
V=π.AD2.AB=π.a\(^2\).2a=2πa\(^3\)

NA/BA = NC/BC
Vì Tam giác ABC vuông tại A, biết AB=3cm,BC=5cm => AC= 4(cm)
=> NC-NA=4 (cm)
=> NC/BC = NA/BA = ( NC-NA)/(BC-AB) = 2
=> NA= BA*2 =6 (cm)
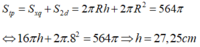
Đáp án B
Ta có diện tích toàn phần của hình trụ: