

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Phương pháp:
- Dựng mặt phẳng chứa B'G và song song với C'D.
- Xác định khối đa diện và tính thể tích bằng cách cộng trừ thể tích các khối đa diện đơn giản.
Cách giải:
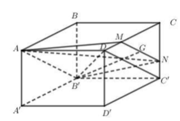

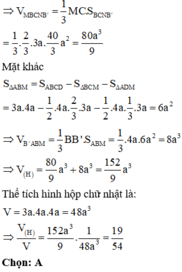

Chọn đáp án C.
Bán kính đáy của khối trụ ngoại tiếp hình hộp chữ nhật đã cho là


Đáp án là B.
+ Ta có: R C = a 3 ⇒ V C = 4 3 π .3 3 a 3 = 4 π a 3 3 .
+ R T = a 2 ⇒ V T = 2 a .. π 2 a 2 = 4 π a 3
Vậy V C V T = 3 .

Đáp án B
Thể tích khối cầu ngoại tiếp tứ diện ABCD’ chính là thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A’B’C’D’. Khi đó, bán kính khối cầu ngoại tiếp là R = A C ' 2 .
Ta có V = 4 3 πR 3 = 4 3 π . AC ' 3 8 = 9 2 πa 3 ⇒ AC ' 3 = 27 a 3 ⇒ AC ' = 3 a .
Mặt khác A C ' 2 = A B 2 + A D 2 + A A ' 2 ⇒ A D 2 = ( 3 a 2 ) - a 2 - ( 2 a ) 2 = 4 a 2 ⇒ A D = 2 a .
Vậy thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là V = A A ' . A B . A D = a . 2 a . 2 a = 4 a 3 .

Đáp án C
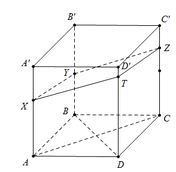
Ta có: V A ' B ' C ' D ' . X Y Z T V A ' B ' C ' D ' . A B C D = 1 2 A ' X A ' A + C ' Z C ' C = 1 2 . 1 3 + 1 4 = 7 24
Cho V X Y Z T . A ' B ' C ' D ' = 7 ; V A ' B ' C ' D ' . A B C D = 24
Khi đó V X Y Z T . A B C D = 17 ⇒ k = 17 7 .