Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\text{Δ}ABC\sim\text{Δ}HBA;\text{Δ}ABC\sim\text{Δ}HCA\)
b: \(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
\(BH=\dfrac{AB^2}{BC}=\dfrac{15^2}{25}=9\left(cm\right)\)
CH=BC-BH=25-9=16(cm)

gọi H, K là trung điểm AB, AC thì HK là đường tb của hình thang DMNE. HK=(DM+EN)/2
Bc=2HK

Đáp án C
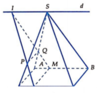
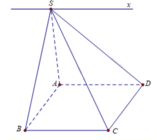
Gọi d là giao tuyến của hai mặt phẳng (SAB) và (SCD).
Ba mặt phẳng (SAB),(SCD) và (ABCD) đôi một cắt nhau theo các giao tuyến d; CD; AB. Mà A B / / C D ⇒ d / / A B / / C D ⇒ d là đường thẳng đi qua S và song song với AB và CD =>cố định.
Có I ∈ M Q ⊂ S A B , I ∈ N P ⊂ S C D ⇒ I ∈ d . Vì M là điểm di động trên đoạn AB nên tập hợp các giao điểm I là một đoạn thẳng d. Ta chọn C.

Đáp án D
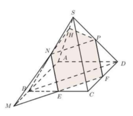
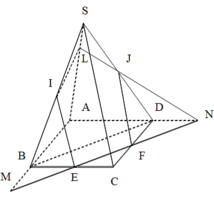
Phương pháp:
Qua M dựng các đường thẳng song song với BD và SC.
Cách giải:

Trong (SAB) kéo dài MN cắt SA tại H.
Vậy thiết diện của chóp khi cắt bởi mặt phẳng (P) là ngũ giác EFPHN.

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

Đáp án D
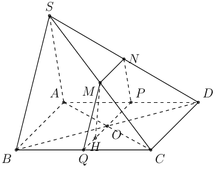
Qua O dựng đường thẳng P Q ∥ A B . Vậy P, Q lần lượt là trung điểm của AD và BC.
Qua P dựng đường thẳng P N ∥ S A . Vậy N là trung điểm của SD
Qua Q dựng đường thẳng Q M ∥ S B . Vậy M là trung điểm của SC.
Nối M và N ⇒ thiết diện của (P) và hình chóp S.ABCD là tứ giác MNPQ.
Vì P Q ∥ C D , M N ∥ C D ⇒ P Q ∥ M N . Vậy tứ giác MNPQ là hình thang.
Ta có P Q = A B = 8 $ , M N = 1 2 A B = 4, M Q = N P = 1 2 S A = 3 . Vậy MNPQ là hình thang cân.
Gọi H là chân đường cao hạ từ đỉnh M của hình thang MNPQ. Khi đó ta có
H Q = 1 4 P Q = 2 ⇒ M H = M Q 2 − H Q 2 = 5
Vậy diện tích của thiết diện cần tìm là S = ( M N + P Q ) M H 2 = 6 5 .


Đáp án B