Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Phương pháp:
- Xác định chân đường cao của đỉnh S đến mặt phẳng đáy.
- Tính thể tích khối chóp: V = 1 3 S h
Cách giải:
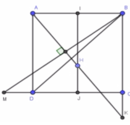
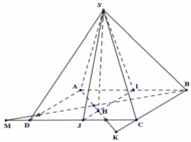
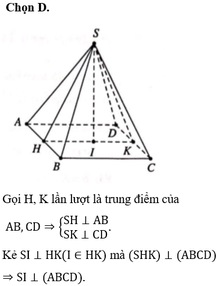
Gọi I, J lần lượt là trung điểm của AB, CD.
Tam giác SAB đều, tam giác SCD cân tại S nên S I ⊥ A B , S J ⊥ C D
Mà A B / / C D ⇒ A B , C D ⊥ S IJ
Dựng S H ⊥ I J , H ∈ I J ⇒ S H ⊥ A B C D (do S H ⊥ I J và S H ⊂ SIJ ⊥ C D )
Trong (ABCD), kẻ
B M ⊥ A H , M ∈ C D , A H ∩ B M = T .
Khi đó, điểm M thỏa mãn điều kiện đề bài.
+) Δ S A B đều, cạnh a ⇒ S I = a 3 2
+) Δ S C D vuông cân tại S,
C D = a ⇒ S J = C D 2 = a 2
+) ABCD là hình vuông cạnh a
⇒ IJ = a
Tam giac SIJ có:
IJ 2 = S I 2 + S J 2 ⇒ Δ S I J vuông tại S.
Mà
S H ⊥ IJ ⇒ SI 2 = I H . IJ ⇒ a 3 2 2 = I H . a ⇒ I H = 3 a 4
Và
1 S H 2 = 1 S I 2 + 1 S J 2 = 1 a 3 2 2 + 1 a 2 2 = 16 3 a 2 ⇒ S H = a 3 4
Dễ dàng chứng minh Δ A I H đồng dạng tam giác
Δ B C M ⇒ S A I H S B M C = A I B C 2 = 1 4 ⇒ S B C M = 4 S A I H = 4. 1 2 . a 2 . 3 a 4 = 3 a 2 4
S B D M = S B C M − S B C D = 3 4 a 2 − 1 2 a 2 = a 2 4
Thể tích khối chóp S.BDM:
V S . B D M = 1 3 . S H . S B D M = 1 3 . a 3 4 . a 2 4 = 3 a 3 48

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

a d e m n b c i h
a, tam giác ade cân a
=> góc d = góc e và ad = ae
tam giác adb = tam giác aec ( cgc)
=> ab=ac
=> tam giác abc cân a
b, tam giác bmd vuông m và tam giác cne vuông n
góc m = góc n =90 độ
góc d = góc e
bd = ce
=> bmd = cne (ch-gn)
=> bm = cn
c, có tam giác bmd = tam giác cne
=> góc mbd = góc nce
mà góc cbi đối đỉnh góc mbd, bci đối đỉnh nce
=> góc cbi = góc bci
=> tam giác ibc cân i
d, lây h là trung điểm bc
tam giác abc cân a có ah là đường trung tuyến úng với bc
=> ah vừa là trung tuyến vừa là đường cao ứng với bc
cmtt với ibc => ih vừa là trung tuyến vừa là đường cao ứng với bc
=> a,i,h thẳng hàng
=> ai vừa trung tuyến vừa là đường cao tam giác abc cân a
=> đpcm

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

\(\left(C_1\right)\) có dạng \(y=x^3-3x\)
Gọi điểm A(a;2) là điểm kẻ đc 3 tiếp tuyến đến C do đề bài yêu cầu tìm điểm thuộc đường thẳng y=2
ta tính \(y'=3x^2-3\)
gọi \(B\left(x_0;y_0\right)\) là tọa độ tiếp điểm
phương trình tiếp tuyến tại điểm B có dạng
\(y=y'\left(x_0\right)\left(x-x_0\right)+y_0\)
suy ra ta có \(y=\left(3x^2_0-3\right)\left(x-x_0\right)+x_0^3-3x_0\)
do tiếp tuyến đi qua điểm A suy ra tọa độ của A thỏa mãn pt tiếp tuyến ta có
\(2=\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0\Leftrightarrow-\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0-2=0\Leftrightarrow-3\left(x_0-1\right)\left(1+x_0\right)\left(a-x_0\right)+\left(1+x_0\right)^2\left(x_0-2\right)=0\)(*)
từ pt * suy ra đc 1 nghiệm \(x_0+1=0\Rightarrow x_0=-1\) hoặc\(-3\left(x_0-1\right)\left(a-x_0\right)+\left(1+x_0\right)\left(x_0-2\right)=0\)(**)
để qua A kẻ đc 3 tiếp tuyến thì pt (*) có 3 nghiệm phân biệt
suy ra pt (**) có 2 nghiệm phân biệt khác -1
từ đó ta suy ra đc a để pt có 2 nghiệm phân biệt khác -1
suy ra đc tập hợ điểm A để thỏa mãn đk bài ra
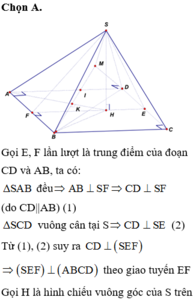

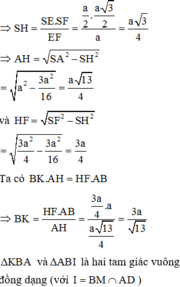

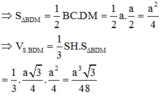


Đáp án A