Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

Đáp án B
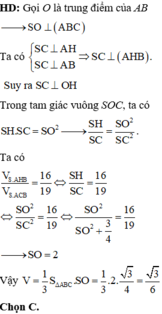
Ta có: O là giao điểm của trục đường tròn ngoại tiếp tam giác ABC và SAB.
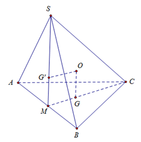
Ta có: O G = 1 3 S M = 3 6 ; M G = C M 3 = 3 6
R = S O = M G 2 + S G 2 = 3 6 + 1 3 = 15 6
Cách 2: Áp dụng CT giải nhanh trong trường hợp S A B ⊥ A B C ta có:
R 2 = R 2 A B C + R 2 S A B − A B 2 4 = 1 2 3 + 1 2 3 − 1 4 = 2 3 − 1 4 = 5 12 ⇒ R = 15 6 .
Vậy V = 4 3 π R 3 = 5 15 π 54 .

Đáp án A
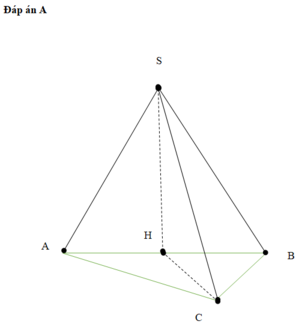
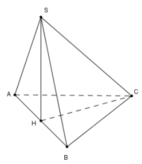
Xét ∆SAB, ta có: SA = SB = a 2 2
ð SH = a 2
Vậy V S . A B C = 1 3 . a 2 . S A B C = 1 3 . a 2 . 1 2 3 2 . a . a = a 3 3 24

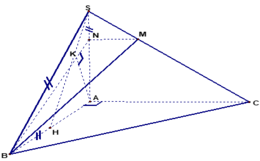
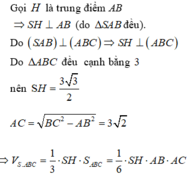
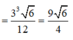
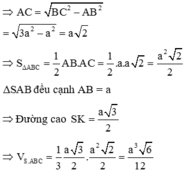


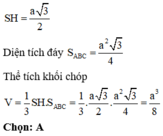
Đáp án C
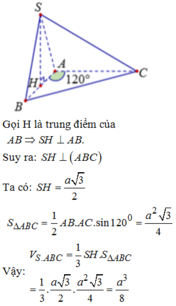
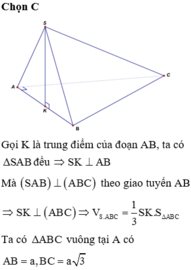
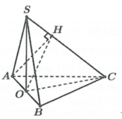
Gọi I là trung điểm của A B ⇒ S I ⊥ A B C
Ta có S I = a 2 − a 2 2 = a 3 2 ; S A B C = 1 2 a 2 sin 60 ° = a 2 3 4
Thể tích của khối chóp S . A B C là:
V = 1 3 S I . S A B C = 1 3 . a 3 2 . a 2 3 4 = a 3 8