Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Một đường thẳng muốn vuông góc với một mặt phẳng thì phải vuông góc với 2 đường thẳng chéo nhau chứ bạn? ở ba câu trên bạn mới chứng minh nó vuông với 1 đường mà

A B C D S E K H
Gọi H là trung điểm của AB, suy ra \(SH\perp\left(ACBD\right)\)
Do đó \(SH\perp HD\) ta có :
\(SH=\sqrt{SD^2-DH^2}=\sqrt{SD^2-\left(AH^2+AD^2\right)}=a\)
Suy ra \(V_{s.ABCD}=\frac{1}{3}.SH.S_{ABCD}=\frac{a^2}{3}\)
Gọi K là hình chiếu vuông góc của H trên BD và E là hình chiếu vuông góc của H lên SK. Ta có :
\(\begin{cases}BD\perp HK\\BD\perp SH\end{cases}\) \(\Rightarrow BH\perp\) (SHK)
=> \(BD\perp HE\) mà \(HE\perp SK\) \(\Rightarrow HE\perp\) (SBD)
Ta có : HK=HB.\(\sin\widehat{KBH}\)\(=\frac{a\sqrt{2}}{4}\)
Suy ra \(HE=\frac{HS.HK}{\sqrt{HS^2+HK^2}}=\frac{a}{3}\)
Do đó \(d\left(A:\left(SBD\right)\right)\)=2d(H; (SBD)) =3HE=\(\frac{2a}{3}\)

Chọn đáp án D.
Ta có: ![]()
Kẻ 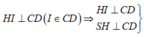
![]()
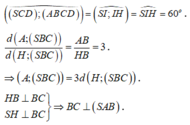
Kẻ ![]()
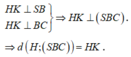
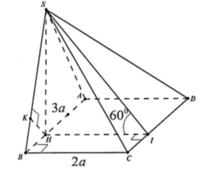
Xét tam giác SHI vuông tại H:
![]()
![]()
Xét tam giác SHB vuông tại B: 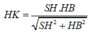
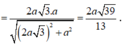
![]()
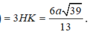

S H B K A I C D
Gọi K là hình chiếu của I lên AB
Suy ra \(\widehat{SKI=60^0}\)
Mà \(\frac{BI}{ID}=\frac{BC}{AD}=\frac{a}{3a}=\frac{1}{2}\)\(\Rightarrow\frac{BI}{BI+ID}=\frac{1}{4}\)\(\Rightarrow\frac{BI}{BD}=\frac{1}{4}\)
Suy ra \(\frac{KI}{DA}=\frac{1}{4}\)\(\Rightarrow KI=\frac{3a}{4}\Rightarrow SI=\frac{3a\sqrt{3}}{4}\)
Do \(IK\) \\ \(AD\Rightarrow\frac{KI}{AD}=\frac{BI}{BD}\)
\(V_{A.ABCD}=\frac{1}{3}.SI.S_{ABCD}=\frac{1}{3}.\frac{3a\sqrt{3}}{4}.\frac{1}{2}\left(a+3a\right)a=\frac{a^3\sqrt{3}}{2}\)
Gọi H là hình chiếu của I trên SK. Ta có \(\begin{cases}AB\perp IK\\AB\perp SI\end{cases}\)\(\Rightarrow AB\perp IH\)
Từ đó suy ra \(IK\perp\left(SAB\right)\Rightarrow d\left(I,\left(SAB\right)\right)=IK\)
Mà do \(DB=4IB\Rightarrow\left(D,\left(SAB\right)\right)=4d\left(I,\left(SAB\right)\right)=4IH\)
Lại có \(\frac{1}{IH^2}=\frac{1}{IS^2}+\frac{1}{IK^2}=\frac{16}{27a^2}+\frac{16}{9a^2}=\frac{64}{27a^2}\Leftrightarrow IH=\frac{3a\sqrt{3}}{8}\)
Vậy \(d\left(D,\left(SAB\right)\right)=\frac{3a\sqrt{3}}{2}\)

D A B C N M I G H
\(d\left(M,BN\right)=\frac{\left|13\left(-1\right)-10.2+13\right|}{\sqrt{13^2+10^2}}=\frac{20}{\sqrt{269}}\)
\(H\in\Delta\Leftrightarrow H\left(3a;2a\right)\)
Gọi I là tâm ABCD, G là giao điểm của AC và BN. Ta thấy G là trọng tâm của tam giác BCD
Suy ra \(CG=\frac{2}{3}.CI=\frac{1}{3}AC\) mà \(AM=\frac{1}{4}AC\Rightarrow MG=\frac{5}{12}AC\Rightarrow CG=\frac{4}{5}MG\)
\(\Rightarrow d\left(C,BN\right)=\frac{4}{5}d\left(M,BN\right)=\frac{16}{\sqrt{269}}\Rightarrow d\left(H,BN\right)=2d\left(C,BN\right)=\frac{32}{\sqrt{269}}\)
\(\Leftrightarrow\frac{\left|13.3a-10.2a+13\right|}{\sqrt{269}}=\frac{32}{\sqrt{269}}\Leftrightarrow a=1\) hoặc \(a=\frac{-45}{19}\)
Vì H và M nằm khác phía đối với đường thẳng BN nên \(H\left(3;2\right)\)
Tiếp.........
Ta thấy \(CM=\frac{3AC}{4}=\frac{2AB}{4}=\frac{2CD}{4}=\frac{CD}{2}=CD=CH\Rightarrow\Delta MHN\) vuông tại M
HM có phương trình \(y-2=0\Rightarrow MN:x+1=0\Rightarrow N\left(-1;0\right)\Rightarrow C\left(1;1\right),D\left(-3;-1\right)\)
Do \(\overrightarrow{CM}=3\overrightarrow{MA}\Rightarrow A\left(\frac{-5}{3};\frac{7}{3}\right)\Rightarrow I\left(\frac{-1}{3};\frac{5}{3}\right)\Rightarrow B\left(\frac{7}{3};\frac{13}{3}\right)\)
Vậy \(A\left(\frac{-5}{3};\frac{7}{3}\right);B\left(\frac{7}{3};\frac{13}{3}\right);C\left(1;1\right);D\left(-3.-1\right)\)



Chọn đáp án C
HC là hình chiếu của SC lên mặt phẳng (ABCD).
Góc giữa SC với mặt phẳng (ABCD) là: S C H ^ = 45 °
Kẻ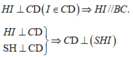
Kẻ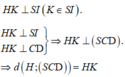
Ta có: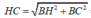
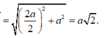
Tam giác SHC vuông cân tại H vì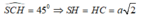
Mặt khác: HI = AD = a
Xét tam giác SHI vuông tại H: