Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
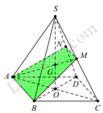
Gọi G là trọng tâm của tam giác SAC và AG cắt SC tại M =>M là trung điểm của SC, tương tự N là trung điểm của SD. Do đó, mp (P) cắt khối chóp theo thiết diện là tứ giác ABMN.
Ta có
V S . A M N V S . A C D = S M S C . S N S D = 1 4 ; V S . A B M V S . A B C = 1 2 ⇒ V S . A B M N V S . A B C D = 3 8 .
Suy ra
V S . A B M N = 3 8 . 1 3 . S O . S A B C D = a 8 . tan 60 ∘ . 2 a 2 = a 3 3 2 .

Đáp án C

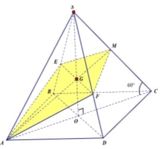
Gọi O = A C ∩ B D , G = A O ∩ A C '
Ta có A C ⊥ ( S B D ) mặt khác S C ⊥ B ' D ' ⇒ B ' D ' ⊥ ( S A C ) ⇒ B ' D ' / / B D
Theo Định lý Talet ta có S B ' B ' B = S D ' D ' D = S G G O = 2 ⇒ G là trọng tâm ∆ S A C ⇒ C ' là trung điểm SC
Vậy V S A B ' C ' D ' V S A B C D = V S A B ' C ' + V S A C ' D ' V S A B C D = 1 2 ( V S A B ' C ' V S A B C + V S A C ' D ' V S A C D ) = 1 2 S B ' . S C ' S B . S C + S C ' . S D ' S C . S D

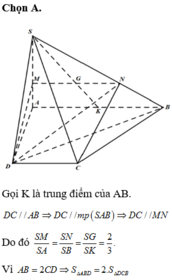
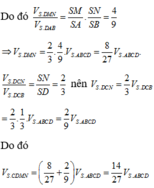
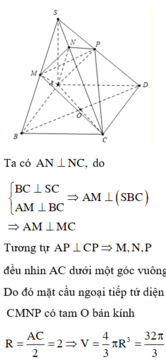
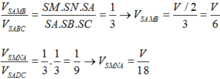
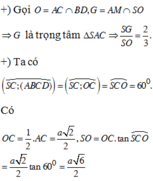

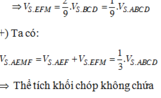
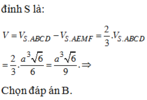


Chọn C.
Phương pháp : Sử dụng tỉ số thể tích.