Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

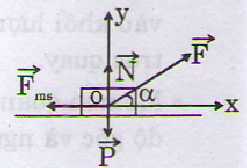
Lực tác dụng lên vật m được biểu diễn trên hình vẽ.
Định luật II Niu-tơn cho:
Chọn hệ trục Oxy với chiều dương là chiều chuyển động theo phương Ox, chiếu phương trình (1) lên:
(Ox): Fcosα- fms= ma (2)
(Oy): N + Fsinα – P = 0 (3)
mà fms= μN (4)
(2), (3) và (4) => F cosα – μ(P- Fsinα ) = ma
=> Fcosα – μP + μFsinα = ma
F(cosα +μsinα) = ma +μmg
=> F =
a) khi a = 1,25 m/s2


Vì vật chuyển động đều
\(\Rightarrow\overrightarrow{F}+\overrightarrow{N}+\overrightarrow{P}+\overrightarrow{F_{ms}}=\overrightarrow{0}\)
Chọn trục toạ độ có trục hoành hướng sang phải, trục tung hướng lên
\(\Rightarrow\left\{{}\begin{matrix}Ox:F.\cos\alpha-F_{ms}=0\\Oy:F.\sin\alpha+N-P=0\end{matrix}\right.\)
\(\Rightarrow F.\cos\alpha-\mu.\left(P-F.\sin\alpha\right)=0\)
\(\Leftrightarrow120.\cos60-\mu.\left(200-120.\sin60\right)=0\)
=> \(\mu=...\)
Tìm gia tốc trong trường hợp alpha= 300 thì lúc này vật chuyển động biến đổi đều nên có gia tốc, tức là \(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
Cậu chiếu lên trục toạ độ rồi phân tích, bt hệ số ma sát rồi thì tìm a ez

a) Gọi m là khối lượng hàng hóa trên xe.
Theo đề bài, ta có: \(F=0,3\times1500=450N\)
lại có \(F=0,2\times\left(m+1500\right)\)= 450
giải phương trình trên, ta được m = 750 kg
==> Vậy khối lượng hàng hóa trên xe là 750 kg

chọn hệ trục xOy như hình vẽ ta có
các lực tác dụng lên vật là: \(\overrightarrow{Fms},\overrightarrow{F},\overrightarrow{P},\overrightarrow{N}\)
theo định luật 2 Newton ta có
\(\overrightarrow{F}+\overrightarrow{Fms}+\overrightarrow{P}+\overrightarrow{N}=\overrightarrow{a}.m\left(1\right)\)
chiếu phương trình 1 lên trục Oy ta có
-P + N=0
\(\Leftrightarrow\)P=N\(\Rightarrow\)Fms=\(\mu.N=\mu.mg\)
chiếu pt 1 lên trục Ox ta có
F-Fms=am
\(\Rightarrow\)F=am-Fms=a.m-\(\mu mg\)=1,25.10-0,3.4.10=0,5(N)
Vậy ..........
O x y P N Fms F

2) ta có : \(\left\{{}\begin{matrix}v_0+a\left(3-\frac{1}{2}\right)=8\\v_0+a\left(6-\frac{1}{2}\right)=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}v_0+\frac{5}{2}a=8\\v_0+\frac{11}{2}a=2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}-3a=6\\v_0+\frac{5}{2}a=8\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=-2\left(m/s^2\right)\\v_0=13m/s\end{matrix}\right.\)
=> Chọn D.
Bài1:
\(S_1=v_0.2-\frac{1}{2}.a2^2=20\)
=> \(2v_0-2a=60\)(1)
\(v^2-v_0^2=2as\Rightarrow0^2-v_0^2=2a.20\Rightarrow v_0=\sqrt{40a}\)(2)
Từ (1) và (2) => \(2.\sqrt{40a}-2a=60\)
=> \(2\left(\sqrt{40a}-a\right)=60\)
<=> \(\sqrt{40a}-a=30\)
<=> \(\sqrt{40a}=30+a\Leftrightarrow40a=a^2+60a+900\)
=> \(a^2+20a+900=0\) (pt vô nghiệm)

Câu 2: Một người kéo một thùng nước có khối lượng 15kg từ giếng sâu h=8m lên, chuyển động nhanh dần đều trong 4s. lấy \(g=10m/s^2\) Tính công và công suất của người đó.
_______________________________________________
\(h=\frac{1}{2}at^2\)
\(8=\frac{1}{2}a.4^2\)
\(a=1m/s\)
\(F-P=ma\)
\(F=ma+P=15.1+15.10=165N\)
\(A=Fs=165.8=20,625J\)
\(P=\frac{A}{t}=\frac{20,625}{4}=5,15625W\)
Vậy ............
Câu 1
\(p=\sqrt{p_1^2+P_2^2}=\sqrt{\left(1.3\right)^2+\left(4.1\right)^2}=5\)
Câu 2
\(m=15\left(kg\right)\)
\(h=S=8m\)
\(t=4s\)
\(g=10\left(\frac{m}{s^2}\right)\)
a. Tính A = ?
Quãng đường mà thùng nước đi được :
\(S=\frac{1}{2}at^2\rightarrow a=\frac{2S}{t^2}=\frac{2.8}{4^2}=1\left(\frac{m}{s^2}\right)\)
Theo định luật II Niuton ta có : vectoP + vectoF = m.vecto a
\(\rightarrow F=P+ma\)
\(\rightarrow F=mg+ma\)
\(\rightarrow F=15.10+15,1=165\left(N\right)\)
- Công của lực kéo tính theo công thức : \(A=F.S\)
\(\rightarrow A=F.S\)
\(\rightarrow A=165.8=1320\left(J\right)\)
b . Tính: P = ?
- Công suất của người ấy tính theo công thức : \(P=\frac{A}{t}\)
\(\rightarrow P=\frac{1320}{4}=330\left(W\right)\)

Câu 2 :
a/\(Wt1−Wt2=m.g.z1−m.g.z2=m.g.(z1+z2)=3.10.(z1+z2)=30(z1+z2)(J)\)mà \(W_{t1}-W_{t2}=500-(-900)=1400(J)\Rightarrow Z=Z_{1}+Z_{2}=\frac{1400}{30}\approx 46,6(m)\)b/Tại vị trí ứng với mức thế năng bằng 0 thì z = 0
thế năng tại vị trí z1 là \(Wt1=m.g.z1⇒z1=5003.10≈16,6(m)\)
vậy vị trí ứng với mức không của thế năng đã chọn cách điểm thả vật 1 khoảng 16,6m
c)ta có
\(v2−v20=2.g.z1⇒v=2.g.z1√=2.10.16,6√=283√(m/s)\)

Đáp án C
Theo định luật II Niu tơn, ta có: