Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

Đáp án D
Phương trình hoành độ giao điểm của )C) và(d) là
x + 2 x = x + m ⇔ x ≠ 0 x 2 + m − 1 x − 2 = 0 *
Để (C) cắt (d) tại 2 điểm phân biệt ⇔ * có 2 nghiệm phân biệt khác 0 ⇔ m ∈ ℝ
Khi đó, gọi A x 1 ; x 1 + 1 ; B x 2 ; x 2 + m ⇒ x 1 + x 2 = 1 − m là tọa độ giao điểm của (C) và(d)
Ta có: A B → = x 2 − x 1 ; x 2 − x 1 ⇒ u A B → = 1 ; 1 ; trung điểm AB là: I 1 − m 2 ; 1 + m 2
m = 0 ⇒ M , A , B thẳng hang (loại m = 0 )
Phương trình trung trực là: x + y − 1 = 0
Do M ∈ d ⇒ Δ M A D luôn cân tại M
Kết hợp với m ∈ ℤ và có 2018 giá trị m cần tìm

Chọn đáp án A
Phương pháp
Nhẩm nghiệm của phương trình hoành độ giao điểm, từ đó tìm điều kiện để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.

Để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt thì phương trình x 2 + ( m + 3 ) x + m 2 = 0 phải có hai nghiệm phân biệt khác 1
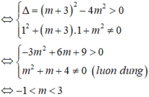
Do đó với -1<m<3 thì đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt
![]()

Phương trình tiếp tuyến tại M0 có dạng: y = k(x – x0) + y0 (*)
Với x0 là hoành độ tiếp điểm;
Với y0 = f(x0) là tung độ tiếp điểm;
Với k = y’(x0) = f’(x0) là hệ số góc của tiếp tuyến.
Để viết được phương trình tiếp tuyến ta phải xác định được x0; y0 và k


Đáp án B.
Phương pháp: Tìm điều kiện để phương trình hoành độ giao điểm có ba nghiệm phân biệt thỏa mãn x A = 2 , hoặc x B < - 1 < x C < 1 hoặc - 1 < x B < 1 < x C
Cách giải:
Đồ thị hàm số y = x 3 - 2 ( m + 1 ) x 2 + ( 5 m + 1 ) x - 2 m - 2 luôn đi qua điểm A(2;0)
Xét phương trình hoành độ giao điểm
x 3 - 2 ( m + 1 ) x 2 + ( 5 m + 1 ) x - 2 m - 2 = 0
Để phương trình có 3 nghiệm phân biệt ó pt (*) có 2 nghiệm phân biệt khác 2
Giả sử x B ; x C ( x B < x C ) là 2 nghiệm phân biệt của phương trình (*).
Để hai điểm B, C một điểm nằm trong một điểm nằm ngoài đường tròn x2 + y2 = 1
TH1: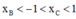
TH2: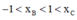
Kết hợp điều kiện ta có: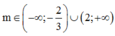
Lại có m ∈ [–10;100]
=> Có 108 giá trị m nguyên thỏa mãn yêu cầu bái toán