Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn: D
![]()
![]()
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x 0 là:
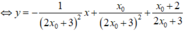
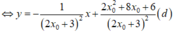
Cho x = 0
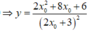
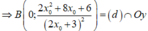
Cho y = 0
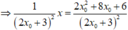
![]()
![]()
∆ O A B c â n t ạ i O ⇔ O A = O B
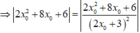
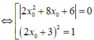
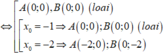
Với x 0 = - 2
![]()
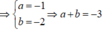

Gọi k là hệ số góc của tiếp tuyến tại M, N thì \(x_M;x_N\) là nghiệm của phương trình :
\(f'\left(x\right)=k\Leftrightarrow3x^2-6x-k=0\)
Để tồn tại hai tiếp điểm M, N thì phải có \(\Delta'>0\Leftrightarrow k>-3\)
Ta có \(y=f'\left(x\right)\left(\frac{1}{3}x-\frac{1}{3}\right)-2x+2\)
Từ \(f'\left(x_M\right)=f'\left(x_N\right)=k\) suy ra phương trình đường thẳng MN là :
\(y=\left(\frac{k}{3}-2\right)x+2-\frac{k}{3}\), khi đó \(A\left(1;0\right);B\left(0;\frac{6-k}{3}\right)\)
Ta có \(AB^2=10\Leftrightarrow k=15\) (do k > -3)
Từ đó ta có 2 tiếp tuyến cần tìm là :
\(y=15x-12\sqrt{6}-15\)
\(y=15x+12\sqrt{6}-15\)

Tập xác định : \(D=R\backslash\left\{1\right\}\)
Ta có \(y'=\frac{-1}{\left(x-1\right)^2}\).
Gọi \(M\left(x_o;y_0\right)\) là tiếp điểm
a) Ta có \(y_0=0\Rightarrow x_0=\frac{1}{2}\Rightarrow y'\left(x_0\right)=-4\)
Phương trình tiếp tuyến là : \(y=-4x+2\)
b) Phương trình hoành độ giao điểm của d và (C) :
\(\frac{2x-1}{x-1}=x+1\Leftrightarrow x^2-2x=0\Leftrightarrow x=0;x=2\)
* \(x_0=0\Rightarrow\) phương trình tiếp tuyến là : \(y=-x\left(x-0\right)+1=-x+1\)
* \(x_0=2\Rightarrow\) phương trình tiếp tuyến là : \(y=-x+5\)
c) Ta có phương trình của đường thẳng \(\Delta:y-\frac{2x_0-1}{x_0-1}=\frac{-1}{\left(x_0-1\right)^2}\left(x-x_0\right)\)
hay \(\Delta:\frac{1}{\left(x_0-1\right)^2}x+y-\frac{x_0}{\left(x_0-1\right)^2}-\frac{2x_0-1}{x_0-1}=0\)
Ta có : \(d\left(I;\Delta\right)=\frac{\left|\frac{2}{x_0-1}\right|}{\sqrt{\frac{1}{\left(x_0-1\right)^4}+1}}\le\sqrt{2}\)
Đẳng thức xảy ra \(\Leftrightarrow\left(x_0-1\right)^4=1\Leftrightarrow\left[\begin{array}{nghiempt}x_0=0\\x_0=2\end{array}\right.\)
Suy ra có 2 tiếp tuyến là : \(\Delta_1:y=-x+1\)
\(\Delta_2:y=-x+5\)
d) Ta có : \(\Delta Ox=A\left(2x^2_0-2x_0+1;0\right)\)
\(OA=1\Leftrightarrow\left|2x^2_0-2x_0+1\right|=1\Leftrightarrow\left[\begin{array}{nghiempt}x_0=0\\x_0=1\end{array}\right.\)
Suy ra phương trình tiếp tuyến là : \(y=-x+1\)

Phương trình hoành độ giao điểm \(3x^2+2mx+3m-4=0\left(1\right)\) với x. Đường thẳng d cắt đồ thị (C) tại hai điểm phân biệt khi và chỉ khi phương trình (1) có 2 nghiệm phân biệt khác -1
\(\Leftrightarrow\begin{cases}9m^2-36m+48>0\\0.m-1\ne0\end{cases}\) (đúng với mọi m)
Gọi \(x_1;x_2\) là các nghiệm của phương trình (1), ta có : \(\begin{cases}x_1+x_2=-m\\x_1x_2=\frac{3m-4}{3}\end{cases}\) (*)
Giả sử \(A\left(x_1;x_1+m\right);B\left(x_2;x_2+m\right)\)
Khi đó ta có \(OA=\sqrt{x^2_1+\left(x_1+m\right)^2};OA=\sqrt{x^2_2+\left(x_2+m\right)^2}\)
Kết hợp (*) ta được \(OA=OB=\sqrt{x_1^2+x_2^2}\)
Suy ra tam giác OAB cân tại O
Ta có \(AB=\sqrt{2\left(x_1-x_2\right)^2}\). Tam giác OAB đều \(\Leftrightarrow OA^2=AB^2\Leftrightarrow x_1^2+x_2^2=2\left(x_1-x_2\right)^2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-6x_1x_2=0\)
\(\Leftrightarrow m^2-6m+8=0\Leftrightarrow m=2\) hoặc m=4

+ Gọi M(a; b) là toạ độ của tiếp điểm
Đạo hàm y ' = - 1 ( 2 x + 3 ) 2 < 0 ; ∀ x .
+ Do tam giác OAB cân tại O nên tiếp tuyến ∆ song song với đường thẳng y= -x (vì tiếp tuyến có hệ số góc âm).
Nghĩa là
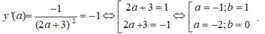
-Với a= -1; b= 1 phương trình ∆: y- 1= -( x+ 1) hay y= -x ( loại) .
-Với a= -2; b= 0 thì ∆ : y- 0= -( x+ 2) hay y=-x-2 (nhận).
Vậy phương trình tiếp tuyến cần tìm là y= -x- 2.
Chọn D.

a) Ta có : \(y'=3x^2+2\left(m-1\right)x+m\left(m-3\right)\)
Hàm số (1) có cực đại và cực tiểu nằm 2 phía đối với trục tung <=> phương trình : \(3x^2+2\left(m-1\right)x+m\left(m-3\right)=0\) có 2 nghiệm phân biệt trái dấu
\(\Leftrightarrow P< 0\Leftrightarrow m\left(m-3\right)< 0\Leftrightarrow0< m< 3\)
Vậy \(0< m< 3\) là giá trị cần tìm
b) Khi m = 1 ta có : \(y=x^3-2x\).
Gọi \(M\left(a;a^3-2a\right)\in\left(C\right),a\ne0\)
Ta có \(y'=3x^2-2\) nên hệ số góc của \(\Delta\) là \(y'\left(a\right)=3a^2-2\)
Ta có \(\overrightarrow{OM}\left(a;a^3-2a\right)\) nên hệ số góc đường thẳng OM là \(k=a^2-2\)
Do đó : \(\Delta\perp OM\Leftrightarrow y'_a.k=-1\)
\(\Leftrightarrow\left(3a^2-2\right)\left(a^2-2\right)=-1\Leftrightarrow3a^4-8a^2+5=0\)
\(M_1\left(1;-1\right);M_1\left(-1;1\right);M_3\left(-\frac{\sqrt{15}}{3};\frac{\sqrt{15}}{9}\right);M_4\left(\frac{\sqrt{15}}{3};-\frac{\sqrt{15}}{9}\right)\) \(\Leftrightarrow\left[\begin{array}{nghiempt}a^2=1\\a^2=\frac{5}{3}\end{array}\right.\) \(\Leftrightarrow\left[\begin{array}{nghiempt}a=\pm1\\a=\pm\frac{\sqrt{5}}{3}\end{array}\right.\)(Thỏa mãn)
Suy ra có 4 điểm thỏa mãn đề bài :\(M_1\left(1;-1\right);M_2\left(-1;1\right);M_3\left(-\frac{\sqrt{15}}{3};\frac{\sqrt{15}}{9}\right);M_4\left(\frac{\sqrt{15}}{3};-\frac{\sqrt{15}}{9}\right)\)

Gọi \(M\left(x_0;y_0\right)\) là tiếp điểm của tiếp tuyến \(\Delta\) cần tìm
Ta có : \(y'=3x^2-12x+9\Rightarrow y'\left(x_0\right)=3x^2_0-12x_0+9\)
Ta có : \(x_0=1;y_0=2;y'\left(x_0\right)=0\)
Phương trình tiếp tuyến là : \(y-2=0\left(x-1\right)\) hay y = 2
b) Ta có \(x_0=0\Rightarrow y_0=-2,y'\left(x_0\right)=9\)
Phương trình tiếp tuyến là :\(y+2=9\left(x-0\right)\) hay \(y=9x-2\)
c) Ta có \(x_0=-1\Rightarrow y_0=f\left(x_0\right)=-18;y'\left(x_0\right)=24\)
Phương trình tiếp tuyến là : \(y+18=24\left(x+1\right)\) hay \(y=24x+6\)
d) Ta có : \(y_0=6\Rightarrow x_0^3-6x^2_0+9x_0-2=-2\Leftrightarrow x_0^3-6x^2_0+9x_0=0\)
\(\Leftrightarrow x_0=0;x_0=3\)
* \(x_0=-1\) suy ra phương trình tiếp tuyến là : \(y=9x-2\)
* \(x_0=3\Rightarrow y_0=-2,y'\left(x_0\right)=0\), suy ra phương trình tiếp tuyến là : \(y=2\)
Vậy có 2 tiếp tuyến là \(y=9x-2;y=2\)
e) Ta có : \(y'=0\Leftrightarrow\)\(\begin{cases}x=1\\x=3\end{cases}\)\(y''=6x-12\)
\(y''\left(1\right)=-6< 0;y"\left(3\right)=6>0\)
Suy ra đồ thị (C) có điểm cực tiểu là \(A\left(3;-2\right)\); điểm cực đại là \(B\left(1;2\right)\)
Giả sử \(M\left(a;a^3-6a^2+9a-2\right),a\ne3;1\)
Phương trình đường thẳng AB : \(2x+y-4=0\)
Ta có : \(S_{SBM}=\frac{1}{2}AB.d\left(M;AB\right)=6\)
\(\Leftrightarrow\frac{1}{2}\sqrt{2^2+\left(-4\right)^2}.\frac{\left|2a+a^3-6a^2+9a-2-4\right|}{\sqrt{2^2+1}}=6\)
\(\Leftrightarrow\left|a^3-6a^2+11a-6\right|=6\Leftrightarrow\left[\begin{array}{nghiempt}a=0\Rightarrow M\left(0;-2\right)\\a=4\Rightarrow M\left(4;2\right)\end{array}\right.\)
* Phương trình tiếp tuyến với (C) tại điểm M(0;-2) là : \(y+2=y'\left(0\right)\left(x-0\right)\) hay \(y=9x-2\)
* Phương trình tiếp tuyến với (C) tại điểm M(4;2) là : \(y-2=y'\left(4\right)\left(x-4\right)\) hay \(y=9x-34\)

a. Ta có : \(y'=3x^2-6x+2\)
\(x_0=1\Leftrightarrow y_0=-6\) và \(y'\left(x_0\right)=y'\left(-1\right)=11\)
Suy ra phương trình tiếp tuyến là \(y=y'\left(-1\right)\left(x+1\right)-6=11x+5\)
b. Gọi \(M\left(x_0;6\right)\) là tiếp điểm, ta có :
\(x_0^3-3x_0^2+2x_0=6\Leftrightarrow\left(x_0-3\right)\left(x_0^2+2\right)=0\Leftrightarrow x_0=3\)
Vậy phương trình tiếp tuyến là :
\(y=y'\left(3\right)\left(x-3\right)+6=11x-27\)
c. PTHD giao điểm của (C) với Ox :
\(x^3-3x^2+2x=0\Leftrightarrow x=0;x=1;x=2\)
* \(x=0\) ta có tiếp tuyến : \(y=y'\left(0\right)\left(x-0\right)+0=2x\)
* \(x=1\) ta có tiếp tuyến : \(y=y'\left(1\right)\left(x-1\right)+0=-x+1\)
* \(x=2\) ta có tiếp tuyến : \(y=y'\left(2\right)\left(x-2\right)+0=2x-4\)


