
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

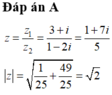


ta có \(A=\frac{yz\sqrt{x-1}+xz\sqrt{y-2}+xy\sqrt{z-3}}{xyz}=\frac{\sqrt{x-1}}{x}+\frac{\sqrt{y-2}}{y}+\frac{\sqrt{z-3}}{z}\)
\(=\sqrt{\frac{1}{x}-\frac{1}{x^2}}+\sqrt{\frac{1}{y}-\frac{2}{y^2}}+\sqrt{\frac{1}{z}-\frac{3}{x^2}}=\sqrt{\frac{1}{4}-\left(\frac{1}{x^2}-2.\frac{1}{2}x+\frac{1}{4}\right)}+\sqrt{\frac{1}{8}-\left(\left(\sqrt{2}y\right)^2-2.\frac{\sqrt{2}}{2\sqrt{2}}x+\frac{1}{8}\right)}+\sqrt{\frac{1}{2}-\left(\left(\sqrt{3}z\right)^2-\frac{1}{z}+\frac{1}{12}\right)}\)
\(=\sqrt{\frac{1}{4}-\left(\frac{1}{x}-\frac{1}{2}\right)^2}+\sqrt{\frac{1}{8}-\left(\frac{\sqrt{2}}{y}-\frac{1}{2\sqrt{2}}\right)^2}+\sqrt{\frac{1}{12}-\left(\frac{\sqrt{3}}{z}-\frac{1}{2\sqrt{3}}\right)^2}\)
ta có \(\sqrt{\frac{1}{4}-\left(\frac{1}{x}-\frac{1}{2}\right)^2}\le\frac{1}{2}\) ; \(\sqrt{\frac{1}{8}-\left(\frac{\sqrt{2}}{y}-\frac{1}{2\sqrt{2}}\right)^2}\le\frac{1}{2\sqrt{2}}\); \(\sqrt{\frac{1}{12}-\left(\frac{\sqrt{3}}{z}-\frac{1}{2\sqrt{3}}\right)^2}\le\frac{1}{2\sqrt{3}}\)
vậy giá trị lớn nhất của A =\(\frac{1}{2}+\frac{1}{2\sqrt{2}}+\frac{1}{2\sqrt{3}}\) khi x=; y=4;z=6

\(M>\frac{x}{x+y+z+t}+\frac{y}{x+y+z+t}+\frac{z}{x+y+z+t}+\frac{t}{x+y+z+t}=\frac{x+y+z+t}{x+y+z+t}=1\)
Mà \(\frac{a}{b}<1\) thì \(\frac{a}{b}<\frac{a+m}{b+m}\) ; \(m\in N\)*
Do đó \(M<\frac{x+t}{x+y+z+t}+\frac{y+z}{x+y+z+t}+\frac{z+x}{x+y+z+t}+\frac{t+y}{x+y+z+t}=\frac{2\left(x+y+z+t\right)}{x+y+z+t}=2\)
Vậy 1 < M < 2 nên M không phải là số tự nhiên/

Chọn đáp án A
Ta có w = z - z ' = 4 + 3 i
⇒ w = 4 2 + 3 2 = 5

Chọn đáp án B
Gọi các kích thước của khối hộp là a (cm), b(cm), c (cm) với a, b, c là các số nguyên dương.
Từ giả thiết ta có
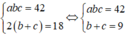
Lại có 9 = b + c ≥ 2 b c ⇒ b c ≤ 81 4
Mà b, c là các số nguyên dương nên b c ≤ 20
Từ b +c =9
⇒ trong hai số b, c có 1 số lẻ và 1 số chẵn ⇒ bc chẵn.
Từ a = 42 b c và a nguyên dương nên bc là ước nguyên dương của 42.

Nếu bc =6 thì b, c là nghiệm của phương trình X 2 - 9 X + 6 = 0 (loại vì nghiệm của phương trình này không là số nguyên).
Nếu bc =14 thì b, c là nghiệm của phương trình
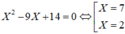
⇒ b c = 14 thỏa mãn. Vậy chiều cao của khối hộp là a = 42 b c = 3 c m