Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Gọi mặt phẳng cần tìm là (P). Khi đó (P) nhận vtpt của α và β là cặp vtcp
![]()
![]()
![]()

Mặt phẳng ( α ) vuông góc với hai mặt phẳng ( β ) và ( γ ), do đó hai vecto có giá song song hoặc nằm trên ( α ) là: n β → = (3; −2; 2) và n γ → = (5; −4; 3).
Suy ra n α → = n β → ∧ n γ → = (2; 1; −2)
Mặt khác ( α )( α ) đi qua điểm M(3; -1; -5) và có vecto pháp tuyến là n α → . Vậy phương trình của ( α ) là: 2(x – 3) + 1(y + 1) – 2(z + 5) = 0 hay 2x + y – 2z – 15 = 0.

Đáp án B
Mặt phẳng (α) song song với mặt phẳng (β) khi và chỉ khi:
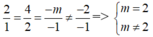
Hệ này vô nghiệm nên không có giá trị của m thỏa mãn.

a) Vector pháp tuyến của hai mặt phẳng (\(\alpha\)) và (\(\beta\)) lần lượt là \(\overrightarrow{n_{\alpha}}\)=(4;1;2) và \(\overrightarrow{n_{\beta}}\)=(2; -2;1). Do hai vector này không cùng phương nên hai mặt phẳng (\(\alpha\)) và (\(\beta\)) cắt nhau.
b) Với x=0, \(\left\{{}\begin{matrix}y+2z+1=0\\-2y+z+3=0\end{matrix}\right.\)⇒ \(\left\{{}\begin{matrix}y=1\\z=-1\end{matrix}\right.\).
Với x=1, \(\left\{{}\begin{matrix}4+y+2z+1=0\\2-2y+z+3=0\end{matrix}\right.\)⇒ \(\left\{{}\begin{matrix}y=1\\z=-3\end{matrix}\right.\).
Suy ra đường thẳng d đi qua hai điểm A(0;1; -1) và B(1;1; -3), \(\overrightarrow{u_d}\)=\(\overrightarrow{AB}\)=(1;0;-2).
Phương trình cần tìm:
d: \(\left\{{}\begin{matrix}x=t\\y=1\\z=-1-2t\end{matrix}\right.\).
c) Gọi M'(x;y;z). Phương trình đường thẳng d' đi qua M(4;2;1) và nhận vector \(\overrightarrow{n_{\alpha}}\)=(4;1;2) làm vector chỉ phương là:
d': \(\left\{{}\begin{matrix}x=4+4t\\y=2+t\\z=1+2t\end{matrix}\right.\). Gọi M"(4+4t; 2+t; 1+2t) ∈ d'.
M"=d'\(\cap\)(α) ⇒ 4(4+4t)+2+t+2(1+2t)+1=0 ⇒ t= -1 ⇒ M''(0;1; -1).
Điểm M' đối xứng với M qua M'', suy ra M'(-4;0; -3).
d) Gọi N'(a;b;c). Phương trình mp(P) đi qua N(0;2;4) và nhận vector \(\overrightarrow{u_d}\)=(1;0; -2) làm vector pháp tuyến là:
(P): x -2z+8=0. Gọi N''(t;1; -1 -2t) ∈ d.
N''=d\(\cap\)(P) ⇒ t -2( -1 -2t)+8=0 ⇒ t= -2 ⇒ N''(-2;1;3).
Điểm N' đối xứng với N qua N'', suy ra N'(-4;0;2).


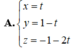
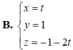
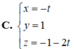
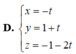

n → α = (1;-2;3); n → β = (2;-4;6)
Hai vecto pháp tuyến của hai mặt phẳng là hai vecto tỉ lệ