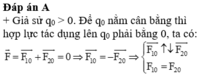Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()
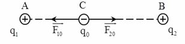
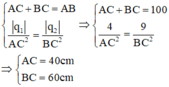
Giả sử q 0 > 0. Để q0 cân bằng thì hợp lực tác dụng lên q 0 phải bằng không, ta có:
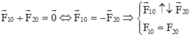
Vì q1; q2 cùng dấu nên C thuộc đoạn thẳng AB: AC + BC = AB (*) và q 1 A C 2 = q 2 B C 2 (**)
Từ (*) và (**) ta có:

1)lực tĩnh điện đẩy nhau cảu A và B là :
9*10^(9)*((1.8*10^(-8)*5.4*10^(-9))/0.03^(2))=9.72*10^(-4) N
gọi X là q c
vì tổng lục tĩnh điện tác dụng lên A ss with BC nên
ta có pt
9.72*10^(-4)+(9*10^(9)*((1.8*10^(-8)*X)/0.04^(2))=9*10^(9)*((5.4*10^(-9)*X)/0.056(2))
giải tìm được X=-1.8*10^(-8)
không chắc đúng đâu !
hình như sai cái gì đó chổ pt thay 0.05^(2) =>0.5^(2)
ta được X=-9.6*10^(-9)

Cường độ điện trường bằng 0 khi:
\(\begin{array}{l}\overrightarrow {{E_1}} + \overrightarrow {{E_2}} = \overrightarrow E = \overrightarrow 0 \Rightarrow \overrightarrow {{E_1}} = - \overrightarrow {{E_2}} \\ \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \\{E_1} = {E_2}\end{array} \right.\end{array}\)
Vì \(\left| {{q_1}} \right| < \left| {{q_2}} \right| \Rightarrow \)Điểm đó thuộc đường thẳng AB và ngoài đoạn AB, gần A hơn (r2>r1)
\(\begin{array}{l}\left\{ \begin{array}{l}{r_2} - {r_1} = AB\\\frac{{r_1^2}}{{r_2^2}} = \frac{{\left| {{q_1}} \right|}}{{\left| {{q_2}} \right|}} = \frac{{\left| {{{3.10}^{ - 6}}} \right|}}{{\left| { - 3,{{5.10}^{ - 6}}} \right|}}\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}{r_1} = 3,6m\\{r_2} = 4,2m\end{array} \right.\end{array}\)
Vậy điểm cần tìm cách A 3,6 m và cách B 4,2 m

Đáp án B.
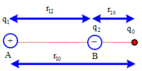
Vì q1 và q2 đặt cố định nên muốn q0 cân bằng thì ba điện tích đặt thẳng hàng, dấu “xen kẽ nhau”, q0 phải ở q0 sẽ chị tác dụng hai lực ngược hướng nhau và độ lớn bằng nhau:
k q 1 q 0 r 10 2 = k q 2 q 0 r 20 2 ⇒ r 10 = 3 r 20 ⇔ r 20 + 12 = 3 r 20 ⇒ r 20 = 6 c m