Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Xét \(\Delta AOK\)và \(\Delta BOK\)có:
\(OA=OB\left(gt\right)\)
\(\widehat{AOK}=\widehat{BOK}\)(Vì Oz là phân giác của \(\widehat{xOy}\))
\(OK\): cạnh chung
Suy ra \(\Delta AOK\)\(=\Delta BOK\)(c.g.c)
\(\Rightarrow AK=BK\)(hai cạnh tương ứng)
Mà K nằm giữa A và B nên K là trung điểm của AB (đpcm)

hình tự vẽ
a, Vì OK là tia phân giác của xOy
=> xOK = KOy = xOy/2
Xét △AOK và △BOK
Có: OA = OB (gt)
AOK = KOB (gt)
OK : cạnh chung
=> △AOK = △BOK (c.g.c)
=> AK = KB (2 cạnh tương ứng)
b, Vì △AOK = △BOK (cmt)
=> AKO = OKB (2 góc tương ứng)
Mà AKO + OKB = 180o (2 góc kề bù)
=> AKO = OKB = 90o
=> OK ⊥ AB

Hình vẽ:

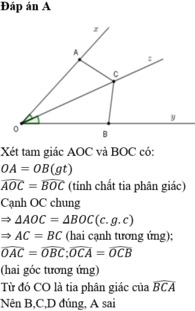
a) Ta có: Oz là tia phân giác của \(\widehat{xOy}\)nên \(\widehat{COA}=\widehat{COB}\)
Xét ΔOAC và ΔOBC có: \(\hept{\begin{cases}OA=OB\left(gt\right)\\\widehat{COA}=\widehat{COB}\left(cmt\right)\\OC.chung\end{cases}}\)=> ΔOAC = ΔOBC (c.g.c)
=> AC = BC (2 cạnh tương ứng)
và \(\widehat{OAC}=\widehat{OBC}\)(2 góc tương ứng)
Ta có: \(\hept{\begin{cases}\widehat{xAC}=\widehat{OAx}-\widehat{OAC}\\\widehat{yBC}=\widehat{OBy}-\widehat{OBC}\end{cases}}\)mà\(\hept{\begin{cases}\widehat{OAx}=\widehat{OBy}\left(=180^o\right)\\\widehat{OAC}=\widehat{OBC}\left(cmt\right)\end{cases}}\)
\(\Rightarrow\widehat{xAC}=\widehat{yBC}\)
b) Gọi H là giao điểm của AB và Ox
Xét ΔOAH và ΔOBH có: \(\hept{\begin{cases}OA=OB\left(gt\right)\\\widehat{COA}=\widehat{COB}\left(cmt\right)\\OH.chung\end{cases}}\)=> ΔOAH = ΔOBH (c.g.c)
=> \(\widehat{OHA}=\widehat{OHB}\)(2 góc tương ứng)
ta có: \(\widehat{AHB}=\widehat{OHA}+\widehat{OHB}=180^o\)mà \(\widehat{OHA}=\widehat{OHB}\)
=> \(\widehat{OHA}+\widehat{OHA}=180^o\Leftrightarrow2\cdot\widehat{OHA}=180^o\Leftrightarrow\widehat{OHA}=90^o\)
=> \(AB\perp Oz\)(đpcm)
Học tốt nha ^3^
giả thiết kết luận đâu bn kẻ hình xong ghi giả thiết, kết luận ms làm chứ![]()

a) Đầu tiên bạn xét tam giác OBD và tam giác OCA = nhau theo trường hợp c.g.c xog suy ra 2 cạnh tương ứng
b) chứng minh AB=DC theo cách cộng đoạn thẳng
chứng minh góc BAE = góc EDC theo cách tổng 3 góc trong 1 tam giác (đầu tiên đưa ra tam giác OBD và tam giác OCA = nhau theo chứng minh trên từ đó suy ra góc B= góc C, sau đó có góc AEB= góc DEC vì đối đỉnh, mà cộng tổng 3 góc trong 1 tam giác luôn =180 độ nên góc BAE = góc EDC)
từ đó xét tam giác ABE=tam giác DCE theo trường hợp g.c.g

Bài giải
1 2 H A C x z y
a) \(\Delta AOC=\Delta BOC\left(c-g-c\right)\)\(\Rightarrow AC=BC\)
và \(\widehat{OAC}=\widehat{OBC}\)mà\(\widehat{OAC}+\widehat{CAx}=180^o\),do đó \(\widehat{xAC}=\widehat{yBC}\)
b) Gọi giao điểm của AB với tia Oz là H,ta có :
\(\Delta OHA=\Delta OHB\left(c-g-c\right)\),do đó \(\widehat{AHO}=\widehat{OHB}\)mà
\(\Delta OHA=\Delta OHB=90^o\)
\(\Rightarrow\)\(AB\perp Oz\)
P/s Hình hơn xấu :)