Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hai mặt phẳng song song (α) và (β) nên có 1 đường thằng a ∈ (α) và a // (β)
⇒ Khoảng cách giữa đường thẳng a và mặt phẳng (β) là bé nhất so với khoảng cách từ một điểm bất kì thuộc a tới một điểm bất kì thuộc mặt phẳng (β).
Vậy khoảng cách giữa hai mặt phẳng song song (α) và (β) là nhỏ nhất trong các khoảng cách từ một điểm bất kì của mặt phẳng này tới một điểm bất kì của mặt phẳng kia.

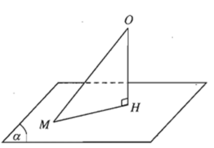
Gọi H là hình chiếu của O lên mặt phẳng (α) ⇒ OH = khoảng cách từ điểm O đến mặt phẳng (α)
M là điểm bất kì thuộc mặt phẳng (α), xét quan hệ giữa đường xiên và hình chiếu OH < OM
Vậy khoảng cách từ điểm O đến mặt phẳng (α) là bé nhất so với các khoảng cách từ O tới một điểm bất kì của mặt phẳng (α).

a) Để tính khoảng cách từ điểm O đến đường thẳng Δ không đi qua O, ta xác định mặt phẳng (O; Δ) và trong mặt phẳng này kẻ OH ⊥ Δ. Độ dài OH chính là khoảng cách từ O đến Δ.
b) Để tính khoảng cách giữa đường thẳng a và mp(α) song song với a, ta lấy một điểm M bất kì thuộc đường thẳng a. Gọi N là hình chiếu của M trên mp(α) . Khoảng cách MN từ điểm M đến mp(α) chính là khoảng cách giữa đường thẳng a và mp(α) song song với a.
c) Để tính khoảng cách giữa hai mp(P) và (P’) song song với nhau, ta lấy một điểm M thuộc (P). Gọi H là hình chiếu của M lên (P’). Khi đó, MH chính là khoảng cách giữa hai mp (P) và (P’).

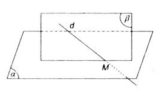
Giả sử có mặt phẳng (β) bất kì chứa đường thẳng d.
M là điểm chung của d và (α) nên:
M ∈ (α) (1)
và M ∈ d, mà d ⊂ (β) ⇒ M ∈ (β) (2).
Từ (1) và (2) suy ra M là điểm chung của (α) và (β).

\(\left. \begin{array}{l}a \bot \left( P \right)\\m \subset \left( P \right)\end{array} \right\} \Rightarrow a \bot m \Rightarrow \left( {a,m} \right) = {90^0}\)
a // b \( \Rightarrow \left( {a,m} \right) = \left( {b,m} \right) = {90^0}\) mà đường thẳng m bất kì thuộc mặt phẳng (P)
\( \Rightarrow \) b \( \bot \) (P).

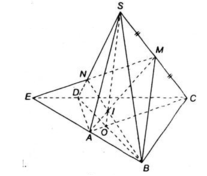
a) + Trong mp(ABCD), AB cắt CD tại E.
E ∈ AB ⊂ (MAB) ⇒ E ∈ (MAB) ⇒ ME ⊂ (MAB)
E ∈ CD ⊂ (SCD) ⇒ E ∈ (SCD)
Mà M ∈ SC ⊂ (SCD)
⇒ ME ⊂ (SCD).
+ Trong mp(SCD), EM cắt SD tại N.
Ta có:
N ∈ SD
N ∈ EM ⊂ mp(MAB)
Vậy N = SD ∩ mp(MAB)
b) Chứng minh SO, MA, BN đồng quy:
+ Trong mặt phẳng (SAC) : SO và AM cắt nhau.
+ trong mp(MAB) : MA và BN cắt nhau
+ trong mp(SBD) : SO và BN cắt nhau.
+ Qua AM và BN xác định được duy nhất (MAB), mà SO không nằm trong mặt phẳng (MAB) nên AM; BN; SO không đồng phẳng.
Vậy SO, MA, BN đồng quy.

Ta có \(MA \bot \left( P \right)\) (A là hình chiếu của M trên (P))
\(NB \bot \left( P \right)\) (B là hình chiếu của N trên (P))
\( \Rightarrow \) MA // NB \( \Rightarrow \) 4 điểm M, A, B, N đồng phẳng
\(\left. \begin{array}{l}\left( {AMNB} \right) \cap \left( P \right) = AB\\a//\left( P \right)\end{array} \right\} \Rightarrow a//AB\)
\( \Rightarrow \) Tứ giác AMNB là hình bình hành.
Mà \(MA \bot AB\left( {MA \bot \left( P \right)} \right)\)
\( \Rightarrow \) Tứ giác AMNB là hình chữ nhật nên MA = NB
Vậy M, N có cùng khoảng cách đến (P).

a) Để tính khoảng cách từ điểm O đến đường thẳng Δ không đi qua O, ta xác định mặt phẳng (O; Δ) và trong mặt phẳng này kẻ OH ⊥ Δ. Độ dài OH chính là khoảng cách từ O đến Δ.
b) Để tính khoảng cách giữa đường thẳng a và mp(P) song song với (P), ta lấy một điểm M bất kì thuộc đường thẳng a. Khoảng cách MN từ điểm M đến mp(P) chính là khoảng cách giữa đường thẳng và mp(P) song song với a.
c) Để tính khoảng cách giữa hai mp(P) và (P') song song với nhau, ta lấy một điểm M thuộc (P) và tìm khoảng cách MH từ điểm M đến mp(P').
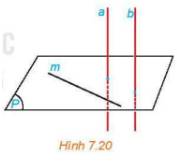

Lấy điểm A ∈ a, A’ là hình chiếu của A trên mặt phẳng (α) ⇒ AA’ = khoảng cách từ A đến mặt phẳng (α)
Mà khoảng cách từ A đến mặt phẳng (α) là bé nhất so với các khoảng cách từ A tới một điểm bất kì của mặt phẳng (α).
Vậy khoảng cách giữa đường thẳng a và mặt phẳng (α) là bé nhất so với khoảng cách từ một điểm bất kì thuộc a tới một điểm bất kì thuộc mặt phẳng (α).