Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
\(A=a_1a_2+a_2a_3+....+a_{n-1}a_n+a_na_1=0\)
Nếu $n$ lẻ, ta thấy tổng $A$ gồm lẻ số hạng, mỗi số hạng có giá trị $1$ hoặc $-1$ nên $A$ lẻ \(\Rightarrow A\neq 0\) (vô lý)
Do đó $n$ chẵn. Nếu $n$ có dạng $4k+2$. Vì $A=0$ nên trong $4k+2$ số hạng trên sẽ có $2k+1$ số có giá trị là $1$ và $2k+1$ số có giá trị $-1$. Vì mỗi số $a_i$ trong $A$ xuất hiện $2$ lần nên \(a_1a_2a_2a_3....a_{n-1}a_na_{n}a_{1}=(a_1a_2...a_n)^2=1^{2k+1}(-1)^{2k+1}=-1\) (vô lý)
Do đó $n$ phải có dạng $4k$, tức là $n$ chia hết cho $4$ (đpcm)

Bài 2:
a) Ta có:
\(S=1-3+3^2-3^3+3^4-3^5+3^6-3^7+...+3^{96}-3^{97}+3^{98}-3^{99}\)
\(=\left(1-3+3^2-3^3\right)+\left(3^4-3^5+3^6-3^7\right)+...+\left(3^{96}-3^{97}+3^{98}-3^{99}\right)\)
\(=1.\left(1-3+3^2-3^3\right)+3^4.\left(1-3+3^2-3^3\right)+...+3^{96}.\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(-20\right)\) \(\text{⋮}\) \(-20\)
Vậy \(S\) \(\text{⋮}\) \(-20\)
Bài 1:
Ta có:
\(A=\left(5m^2-8m^2-9m^2\right).\left(-n^3+4n^3\right)\)
\(=\left[\left(5-8-9\right).m^2\right].\left[\left(-1+4\right).n^3\right]\)
\(=\left(-12\right).m^2.3.n^3\)
\(=\left(m^2.3\right).\left[\left(-12\right)n^3\right]\)
Xét: \(m^2\ge0\) với V m
3>0 nên \(m^2.3\ge0\) với V m
Như vậy để \(A\ge0\) thì \(\left(-12\right)n^3\ge0\)
-12 < 0 nên nếu \(\left(-12\right)n^3\ge0\) thì \(n^3<0\Rightarrow n<0\)
Vậy với n<0 và mọi m thì \(A\ge0\)

Đáp án A.
Ta có
n − 1 n 2 + 3 n + 2 = n − 1 n + 1 n + 2 = A n + 1 + B n + 2 ⇒ A + B = 1 2 A + B = − 1 ⇔ A = − 2 B = 3 .
Lại có 3 u n + 1 = 2 u n − 2 n + 1 + 3 n + 2
⇔ 3 u n + 1 − 1 n + 2 = 2 u n − 1 n + 1 .
Đặt v n = u n − 1 n + 1 ⇒ v 1 = 1 2
và v n = u n − 1 n + 1 → v n
là cấp số nhân với v 1 = 1 2 ; q = 1 3
⇒ v n = 1 2 . 2 3 n − 1 = 3 4 . 2 3 n → u n = v n + 1 n + 1 = 3 4 . 2 3 n + 1 n + 1 = 2 n − 2 3 n − 1 + 1 n + 1 .
⇒ u 2018 = 2 n − 2 3 n − 1 + 1 n + 1 n = 2018 = 2 2016 3 2017 + 1 2019 .

Đáp án A
Ta có u n + 1 2 = u n 2 + 2 = u n - 1 2 + 2 . 2 = u n - 2 2 + 2 . 3 = u 1 2 + 2 n
Do đó S = 1001 u 1 2 + 2 ( 0 + 1 + 2 + . . . + 1000 ) = 1001 + 2 . 1001 . 1000 2 = 1002001 .

Câu 1 : Việc gõ ký hiệu như bạn đề cập ; mình cũng không biết phải làm sao nên cứ dùng xyz vậy thôi.
Ta có:
xyz = 100x +10y +z = 111x -11x +10y +z = 37.3x -(11x-10y-z) chia hết cho 37
=> (11x-10y-z) chia hết cho 37
Lại có:
xyz -yzx = 100x +10y +z -100y -10z -x = 99x -90y -9z = 9.(11x-10y-z) chia hết cho 37
Vậy yzx cũng phải chia hết cho 37
Có thể phát biểu hay hơn là CMR: Khi hoán vị các chữ số của 1 số có 3 chữ số chia hết cho 37 thì được số mới cũng chia hết cho 37.

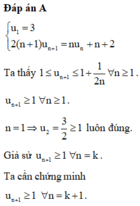
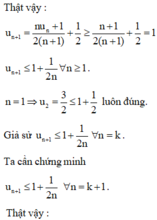
u n + 1 = n u n + 1 2 ( n + 1 ) + 1 2 ≤ n 1 + 1 2 n 2 ( n + 1 ) + 1 2 ≤ 1 + 1 4 ( n + 1 ) ≤ 1 + 1 2 n
suy ra lim u n = 1

Chọn C.
Phương pháp: Dự đoán số hạng tổng quát và chứng minh bằng quy nạp.
Cách giải: Ta có

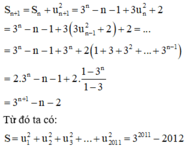
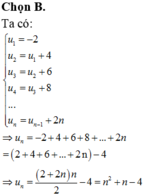
Ta có u 2 = 1 3
Với n ≥ 3 ta có
u 1 + 2 u 2 + . . + n - 1 u n - 1 + n u n = n n 2 - 1 u n + n u n = n 3 u n ⇒ n u n 3 = n u n + n - 1 3 u n - 1 ⇒ u n u n - 1 = n - 1 3 n 3 - n = n - 1 n 2 n n + 1 1
Từ (1) suy ra
u n u 2 = u n u n - 1 . u n - 1 u n - 2 . . . u 3 u 2 = n - 1 n 2 . n - 1 n - 2 2 . . 2 3 2 n n - 1 . n - 1 n . . . 3 4 = 12 n 2 n + 1 ⇒ u n = 4 n 2 n + 1
Vậy l i m n + 2018 3 U n = 4
Đáp án D