Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Lời giải chi tiết:
Giai đoạn 1: (m1; m2) đứng yên lò xo giãn; kết thúc gđ 1 quãng đường đi là:
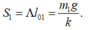
Giai đoạn 2: (m1 đi lên; m2 đứng yên) lò xo không giãn thêm; kết thúc gđ 2 quãng đường đi là:
S 2 = l
Giai đoạn 3: (m1 đi lên; m2 đứng yên) lò xo tiếp tục giãn thêm; kết thúc gđ 3 quãng đường đi là:
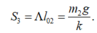
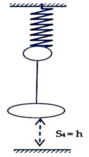
Giai đoạn 4: (m1; m2) cùng đi lên để lại khoảng trống h bằng quãng đường đi được:
S 4 = h
Giai đoạn 5: Dừng đột ngột hệ sẽ dao động điều hòa
Với biên hộ A = v 0 k / ( m 1 + m 2 ) với lực căng dây T C ≥ 0 được thỏa mãn
Như vậy để hệ dao động điều hòa thì khoảng trống h min = S 4 = A
Tương ứng thời gian nhỏ nhất là:
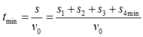
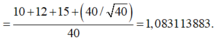

Vận tốc của hai vật sau va chạm: (M + m)V = mv
=> V = 0,02\(\sqrt{2}\) (m/s)
Tọa độ ban đầu của hệ hai vật x0 = \(\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}\) = 0,04m = 4cm
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2+\left(M+m\right)}{k}=0,0016\Rightarrow A=0,04m=4cm\)
→ B
Vận tốc của hai vật sau va chạm: \(\left(M+m\right)V=mv\)
\(\rightarrow V=0,02\sqrt{2}\left(m\text{ /}s\right)\)
Tọa độ ban đầu của hệ hai vật: \(x_0=\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}=0,04m=4cm\)
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2\left(M+m\right)}{k}=0,0016\) \(\rightarrow A=0,04m=4cm\)
Đáp án B

Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm

Các điểm trên lò xo thỏa mãn: \(OM = MN = NI = 10cm.\)
Tỉ số lực kéo lớn nhất và lực kéo nhỏ nhất tác dụng lên điểm treo O của lò xo chính là
\(\frac{F_{đhmax}}{F_{đhmin}} = \frac{k(\Delta l +A)}{k(\Delta l -A)}=3 => \Delta l = 2A.(1)\)
Lò xo dãn đều, khoảng cách lớn nhất giữa hai điểm M, N là 12 cm
=> Độ dãn lớn nhất của cả lò xo là \(\Delta l + A = 3.(12-10) = 6cm. (2)\)
Từ (1) và (2) ta có: \(\Delta l = 4cm = 0,04m.\)
\(T = 2\pi \sqrt{\frac{\Delta l }{g}} = 2\sqrt{\Delta l} = 0,4s.\)
\(f = \frac{1}{T} = 2,5Hz. \)
cho em hỏi : chỗ mà độ dãn lớn nhất của lò xo sao lại ra được vầy ạ ??

\(A=10cm\)
\(\Rightarrow\omega=5\sqrt{2}\)
\(\Rightarrow A_{max}=A-\frac{umg}{k}=0,08\)
\(\Rightarrow v_{max}=A_{max}\omega=0,4\sqrt{2}\left(\frac{m}{s}\right)\)

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)
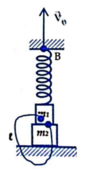

Đáp án A
Độ biến dạng của hệ vật tại vị trí cân bằng ∆ l 0 = m 1 + m 2 k g = 25 c m
Biên độ dao động cùa hệ vật A = v 0 ω = 40 2 10 = 2 10 c m
Để vật có thể dao động điều hòa được thi sợi dây phải ờ trạng thái căng, do đó tổng quãng đường mả vật B phải di chuyển là S = 1 + ∆ l + A = 37 + 2 10 c m
Thời gian tối thiểu t m i n = S v 0 = 1 , 083 s