Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải
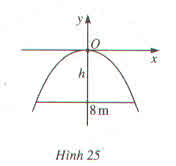
Parabol nhận trục tung là trục đối xứng
(điểm thấp nhất thuộc đồ thị có tọa độ A(4,ya)
\(y\left(4\right)=-\dfrac{1}{2}.4^2=-8\)
Vậy chiều cao cổng là 8m

a) ta có :
\(\Delta'=1^2-\left(-1-m\right)\left(m^2-1\right)=1-\left(-m^2+1-m^3+m\right)=1+m^2-1+m^3-m=m^3+m^2-m=m\left(m^2+m-1\right)\)để phương trình có nghiệm thì \(\Delta\ge0\)
hay \(m\left(m^2+m-1\right)\ge0\)
=> \(\left\{{}\begin{matrix}m\ge0\\m^2+m-1\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\\left(m+\dfrac{1}{2}\right)^2-\dfrac{5}{4}\ge0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m\ge0\\\left(m+\dfrac{1}{2}\right)^2\ge\dfrac{5}{4}\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m\ge0\\\left[{}\begin{matrix}m+\dfrac{1}{2}\ge\\m+\dfrac{1}{2}\le-\dfrac{\sqrt{5}}{2}\end{matrix}\right.\end{matrix}\right.\dfrac{\sqrt{5}}{2}}\)

a) Ta thấy đường thẳng \(y=ax+b\) đi qua hai điểm \(\left(0;3\right)\) và \(\left(1;0\right)\). Vậy ta có :
\(\left\{{}\begin{matrix}3=b\\0=a+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=3\end{matrix}\right.\)
Đường thẳng có phương trình là \(y=-3x+3\)
b) \(y=-4x\)
c) \(y=x-2\)

Bài 1a)
Áp dụng bất đẳng thức Cô-si cho từng cặp ta có
\(\left\{\begin{matrix}a+b\ge2\sqrt{ab}\\b+c\ge2\sqrt{bc}\\c+a\ge2\sqrt{ac}\end{matrix}\right.\)
\(=>\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge2\sqrt{ab}.2\sqrt{bc}.2\sqrt{ac}\)
\(=>\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\sqrt{\left(abc\right)^2}\)
\(=>\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8abc\) ( điều phải chứng minh )
Bài 1b)
Áp dụng bất đẳng thức Cô-si bộ 3 số cho từng cặp ta có
\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\a^2+b^2+c^2\ge3\sqrt[3]{\left(abc\right)^2}\end{matrix}\right.\)
\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\left(abc\right)^2}\)
\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge9\sqrt[3]{\left(abc\right)^3}\)
\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge9abc\) (điều phải chứng minh )
Bài 1c) Ta có
\(\left(1+a\right)\left(1+b\right)\left(1+c\right)\ge\left(1+\sqrt[3]{abc}\right)^3\)
\(=>1+a+b\left(1+a\right)\left(1+c\right)\ge1^3+3.1^2.\sqrt[3]{abc}+3.1.\sqrt[3]{\left(abc\right)^2}+\sqrt[3]{\left(abc\right)^3}\)
\(=>\left(1+a+b+ab\right)\left(1+c\right)\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)
\(=>1+a+b+ab+c\left(1+a+b+ab\right)\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)
\(=>1+a+b+ab+c+ca+bc+abc\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)
\(=>a+b+c+ab+bc+ca\ge3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}\)
Áp dụng bất đẳng thức Cô-si bộ 3 số cho vế trái ta có
\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\ab+bc+ac\ge3\sqrt[3]{\left(abc\right)^2}\end{matrix}\right.\)
\(=>a+b+c+ab+bc+ac\ge3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}\) (điều phải chứng minh )
Bài 2a)
Áp dụng bất đẳng thức Cô-si cho từng cặp ta có
\(\left\{\begin{matrix}\frac{bc}{a}+\frac{ca}{b}\ge2\sqrt{\frac{bc}{a}.\frac{ca}{b}}=2\sqrt{c^2}=2c\\\frac{ca}{b}+\frac{ab}{c}\ge2\sqrt{\frac{ca}{b}.\frac{ab}{c}}=2\sqrt{a^2}=2a\\\frac{bc}{a}+\frac{ab}{c}\ge2\sqrt{\frac{bc}{a}.\frac{ab}{c}}=2\sqrt{b^2}=2b\end{matrix}\right.\)
\(=>2\left(\frac{bc}{a}+\frac{ca}{b}+\frac{ab}{c}\right)\ge2\left(a+b+c\right)\)
\(=>\frac{bc}{a}+\frac{ca}{b}+\frac{ab}{c}\ge a+b+c\) (điều phải chứng minh )
Bài 2b)
Chứng minh BĐT \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)
Áp dụng BĐT Cô-si cho vế trái ta có
\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\sqrt[3]{\frac{1}{abc}}\end{matrix}\right.\)
\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\frac{1}{abc}}\)
\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9.\sqrt[3]{\frac{abc}{abc}}\)
\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\) (điều phải chứng minh )
Ta có \(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\ge\frac{3}{2}\)
\(=>\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}+3\ge\frac{3}{2}+3\)
\(=>\frac{a}{b+c}+1+\frac{b}{a+c}+1+\frac{c}{a+b}+1\ge\frac{9}{2}\)
\(=>\frac{a+b+c}{b+c}+\frac{a+b+c}{a+c}+\frac{a+b+c}{a+b}\ge\frac{9}{2}\)
\(=>\left(a+b+c\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge\frac{9}{2}\)
\(=>2\left(a+b+c\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge9\)
Áp dụng BĐT vừa chứng minh \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)
\(=>\left(b+c+a+c+a+b\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge9 \) (Điều phải chứng minh )

– Các vectơ cùng phương: và
;
,
,
và
;
và
.
– Các vectơ cùng hướng: và
;
,
,
– Các vectơ ngược hướng: và
;
và
;
và
;
và
.
– Các vectơ bằng nhau: =
.

C1:
\(A=\dfrac{10^{50}+2}{10^{50}-1}=\dfrac{10^{50}-1}{10^{50}-1}+\dfrac{3}{10^{50}-1}=1+\dfrac{3}{10^{50}-1}\\ B=\dfrac{10^{50}}{10^{50}-3}=\dfrac{10^{50}-3}{10^{50}-3}+\dfrac{3}{10^{50}-3}=1+\dfrac{3}{10^{50}-3}\\ \text{Vì }10^{50}-3< 10^{50}-1\Rightarrow\dfrac{3}{10^{50}-3}>\dfrac{3}{10^{50}-1}\Rightarrow1+\dfrac{3}{10^{50}-3}>1+\dfrac{3}{10^{50}-1}\Leftrightarrow B>A\)
Vậy \(B>A\)
C2: Áp dụng \(\dfrac{a}{b}>1\Rightarrow\dfrac{a}{b}>\dfrac{a+n}{b+n}\left(n>0\right)\)
Dễ thấy
\(B=\dfrac{10^{50}}{10^{50}-3}>1\\ \Rightarrow B=\dfrac{10^{50}}{10^{50}-3}>\dfrac{10^{50}+2}{10^{50}-3+2}=\dfrac{10^{50}+2}{10^{50}-1}=A\)
Vậy \(B>A\)

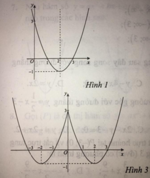
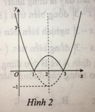
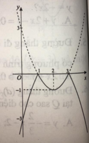






Ta có: y = x 2 - 4 x + 3 = x 2 - 4 x + 3 k h i x 2 - 4 x + 3 ≥ 0 - x 2 - 4 x + 3 k h i x 2 - 4 x + 3 < 0
Cách vẽ đồ thị y = x 2 - 4 x + 3
+ Vẽ đồ thị hàm số y = x2 – 4x + 3 (C).
+ Giữ nguyên phần đồ thị (C) phía trên trục hoành
Lấy đối xứng phần dưới trục hoành qua trục hoành; xóa phần đồ thị (C) dưới trục hoành.
Khi đó, ta được đồ thị hàm số y = x 2 - 4 x + 3 .
Chọn B