Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

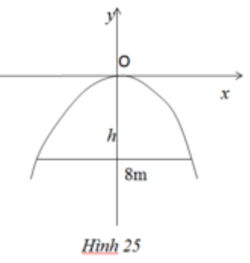
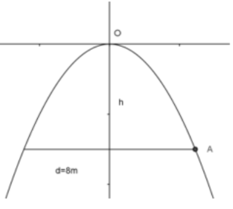
Pra bol đối xứng qua trục Tung => điểm cao nhất thuộc Parabol có tọa độ (2,h)
\(x=2\Rightarrow y=\dfrac{1}{2}\Rightarrow a.2^2=\dfrac{1}{2}\Rightarrow a=\dfrac{1}{8}\)

Có:
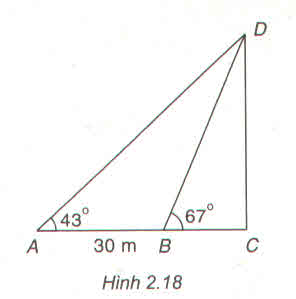
\(DC=AC.tan43^o=\left(AB+BC\right).tan43^o\).
\(DC=BC.tan67^o\).
Vì vây:
\(\left(AB+BC\right).tan43^o=BC.tan67^o\)
\(\Leftrightarrow BC=\dfrac{AB.tan43^o}{tan67^o-tan43^o}=26,55m\).
Suy ra: \(DC=BC.tan67^o=26,55.tan67^o=62,55m\).
Vậy chiều cao DC của chân tháp là 62,55m.

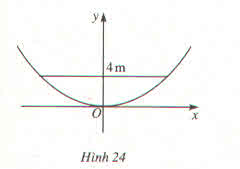
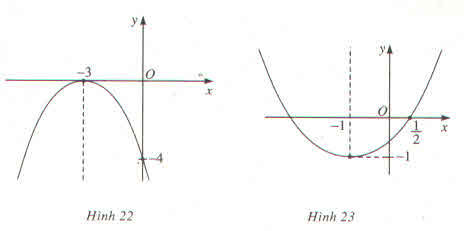
a) Ta thấy đường thẳng \(y=ax+b\) đi qua hai điểm \(\left(0;3\right)\) và \(\left(1;0\right)\). Vậy ta có :
\(\left\{{}\begin{matrix}3=b\\0=a+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=3\end{matrix}\right.\)
Đường thẳng có phương trình là \(y=-3x+3\)
b) \(y=-4x\)
c) \(y=x-2\)

Hình 22
y=ax^2 +bx+c thỏa mãn hệ
\(\left\{{}\begin{matrix}y\left(0\right)=-4\Rightarrow c=-4\\y\left(-3\right)=9a-3b-4=0\\y\left(-6\right)=36a-6b-4=-4\end{matrix}\right.\)
(3) -(2) nhân 2
\(36a-18a-4+8=-4\Rightarrow18a=-8\Rightarrow a=\dfrac{-8}{18}=\dfrac{-4}{9}\)
Thế vào (2) -4-3b-4=0 => b=-8/3
Vậy pa ra bo; cho hình 22 là
\(y=-\dfrac{4}{9}x^2-\dfrac{8}{3}x-4\)

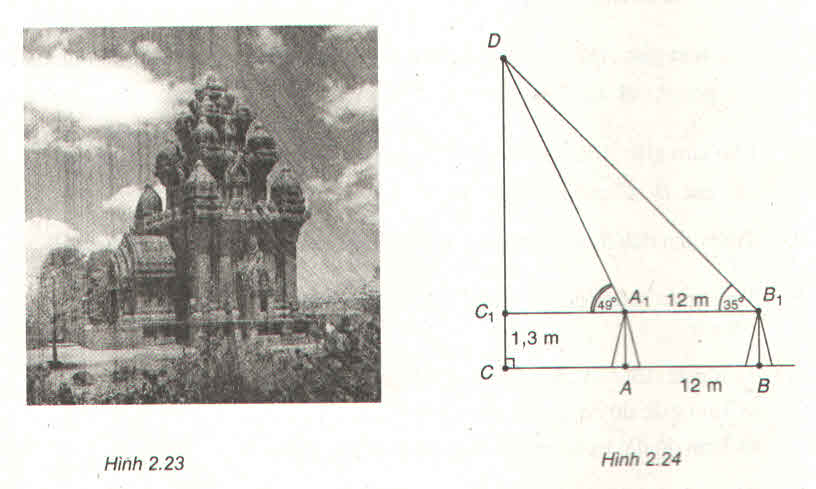
Ta có: Chiều cao của tháp DC = DC1 + C1C = 1,3 + DC1
=> DC = 1,3 + 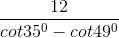
=> DC ≈ 22,8m
cãi đi bé Bài 11 trang 60 sgk hình học 10 - loigiaihay.com

a) \(23,3\) phút; \(540^0;27,6^0C\)
b) Khi lấy số trung bình làm đại diện cho các số liệu thống kê về quy mô và độ lớn, có thể xem rằng mỗi ngày bạn A đi từ nhà đến trường đều mất 23,3 phút.
Tương tự, nêu ý nghĩa số trung bình của các số liệu thống kê cho ở bảng 7 và bảng 8.

a) Bảng phân bố tần số (về tuổi thọ bóng đèn điện) có thể viết dưới dạng như sau:

Số trung bình về tuổi thọ của bóng đèn trong bảng phân bố trên là:
.(3x1150 + 6x1160 + 12x1170 + 6x1180 + 3x1190)
= 1170.
b) Số trung bình về chiều dài lá cây dương xỉ trong bài tập 2 trong là:
.(8x15 + 18x25 + 24x35 + 10x45) = 31 (cm).

Bảng cơ cấu giá trị sản suất công gnhiệp trong nước năm 2000 phân theo thành phần kinh tế (%) dựa theo biểu đồ hình quạt đã cho là:








Lời giải
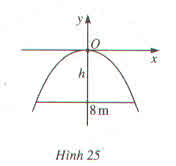
Parabol nhận trục tung là trục đối xứng
(điểm thấp nhất thuộc đồ thị có tọa độ A(4,ya)
\(y\left(4\right)=-\dfrac{1}{2}.4^2=-8\)
Vậy chiều cao cổng là 8m