Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1a)
Áp dụng bất đẳng thức Cô-si cho từng cặp ta có
\(\left\{\begin{matrix}a+b\ge2\sqrt{ab}\\b+c\ge2\sqrt{bc}\\c+a\ge2\sqrt{ac}\end{matrix}\right.\)
\(=>\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge2\sqrt{ab}.2\sqrt{bc}.2\sqrt{ac}\)
\(=>\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\sqrt{\left(abc\right)^2}\)
\(=>\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8abc\) ( điều phải chứng minh )
Bài 1b)
Áp dụng bất đẳng thức Cô-si bộ 3 số cho từng cặp ta có
\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\a^2+b^2+c^2\ge3\sqrt[3]{\left(abc\right)^2}\end{matrix}\right.\)
\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\left(abc\right)^2}\)
\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge9\sqrt[3]{\left(abc\right)^3}\)
\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge9abc\) (điều phải chứng minh )
Bài 1c) Ta có
\(\left(1+a\right)\left(1+b\right)\left(1+c\right)\ge\left(1+\sqrt[3]{abc}\right)^3\)
\(=>1+a+b\left(1+a\right)\left(1+c\right)\ge1^3+3.1^2.\sqrt[3]{abc}+3.1.\sqrt[3]{\left(abc\right)^2}+\sqrt[3]{\left(abc\right)^3}\)
\(=>\left(1+a+b+ab\right)\left(1+c\right)\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)
\(=>1+a+b+ab+c\left(1+a+b+ab\right)\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)
\(=>1+a+b+ab+c+ca+bc+abc\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)
\(=>a+b+c+ab+bc+ca\ge3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}\)
Áp dụng bất đẳng thức Cô-si bộ 3 số cho vế trái ta có
\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\ab+bc+ac\ge3\sqrt[3]{\left(abc\right)^2}\end{matrix}\right.\)
\(=>a+b+c+ab+bc+ac\ge3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}\) (điều phải chứng minh )
Bài 2a)
Áp dụng bất đẳng thức Cô-si cho từng cặp ta có
\(\left\{\begin{matrix}\frac{bc}{a}+\frac{ca}{b}\ge2\sqrt{\frac{bc}{a}.\frac{ca}{b}}=2\sqrt{c^2}=2c\\\frac{ca}{b}+\frac{ab}{c}\ge2\sqrt{\frac{ca}{b}.\frac{ab}{c}}=2\sqrt{a^2}=2a\\\frac{bc}{a}+\frac{ab}{c}\ge2\sqrt{\frac{bc}{a}.\frac{ab}{c}}=2\sqrt{b^2}=2b\end{matrix}\right.\)
\(=>2\left(\frac{bc}{a}+\frac{ca}{b}+\frac{ab}{c}\right)\ge2\left(a+b+c\right)\)
\(=>\frac{bc}{a}+\frac{ca}{b}+\frac{ab}{c}\ge a+b+c\) (điều phải chứng minh )
Bài 2b)
Chứng minh BĐT \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)
Áp dụng BĐT Cô-si cho vế trái ta có
\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\sqrt[3]{\frac{1}{abc}}\end{matrix}\right.\)
\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\frac{1}{abc}}\)
\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9.\sqrt[3]{\frac{abc}{abc}}\)
\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\) (điều phải chứng minh )
Ta có \(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\ge\frac{3}{2}\)
\(=>\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}+3\ge\frac{3}{2}+3\)
\(=>\frac{a}{b+c}+1+\frac{b}{a+c}+1+\frac{c}{a+b}+1\ge\frac{9}{2}\)
\(=>\frac{a+b+c}{b+c}+\frac{a+b+c}{a+c}+\frac{a+b+c}{a+b}\ge\frac{9}{2}\)
\(=>\left(a+b+c\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge\frac{9}{2}\)
\(=>2\left(a+b+c\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge9\)
Áp dụng BĐT vừa chứng minh \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)
\(=>\left(b+c+a+c+a+b\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge9 \) (Điều phải chứng minh )

Ta có : \(0< \alpha< \dfrac{\pi}{2}\)
=> \(\sin\alpha>0,\cos\alpha>\text{0},\tan\alpha>\text{0},\cot\alpha>\text{0}\)
a, Ta có : \(\sin\left(\alpha-\pi\right)=-\sin\left(\pi-\alpha\right)=-\left[-\sin\left(\alpha\right)\right]=\sin\alpha\)
=> \(sin\left(\alpha-\pi\right)>\text{0}\)
b, \(\cos\left(\dfrac{3\pi}{2}-\alpha\right)=\cos\left(\pi+\dfrac{\pi}{2}-\alpha\right)=-\cos\left(\dfrac{\pi}{2}-\alpha\right)=-sin\alpha\)
=> \(\cos\left(\dfrac{3\pi}{2}-\alpha\right)< \text{0}\)
c, \(tan\left(\alpha+\pi\right)=tan\alpha\)
=> \(tan\left(\alpha+\pi\right)>\text{0}\)
d, \(cot\left(\alpha+\dfrac{\pi}{2}\right)=-tan\alpha\)
=> \(cot\left(\alpha+\dfrac{\pi}{2}\right)< \text{0}\)

a) Dạng chuẩn của số π với 10 chữ số chắc là 3,141592654 với sai số tuyệt đối ∆π≤ 10-9.
b) Viết π ≈ 3,14 ta mắc phải sai số tuyệt đối không quá 0,002. Trong cách viết này có 3 chữ số đáng tin.
Viết π ≈ 3,1416 ta mắc phải sai số tuyệt đối không quá 10-4. Viết như vậy thì số π này có 5 chữ số đáng tin.

ta thấy:\(\dfrac{a}{1+b^2}=a-\dfrac{ab^2}{1+b^2}\)
> áp dụng bđt cosi: 1+b2>=2b
>\(a-\dfrac{ab^2}{1+b^2}\ge a-\dfrac{ab^2}{2b}=a-\dfrac{ab}{2}\)
cminh tương tự với \(\dfrac{b}{1+c^2};\dfrac{c}{1+b^2}\)
cộng lần lượt 2 vế ta vừa cminh
>bthức tương đương với: a+b+c-\(\dfrac{ab+bc+ca}{2}\ge3-\dfrac{3}{2}=\dfrac{3}{2}\) đpcminh
(vì (a+b+c)2>=3(ab+bc+ca) hay 32>=3(ab+bc+ca)
> ab+bc+ca<=3)

a) \(\overline{x}=36,5g;s_1-6,73\)
\(M_e=35g;M_0=35g\)
b) Ta chọn số trung bình \(\overline{x}=36,5g\) để làm giá trị đại diện cho các số liệu thống kê đã cho về quy mô và độ lớn
c) Rổ trứng thứ nhất và rổ trứng thứ hai có cùng đơn vị đo và \(\overline{x}_1=\overline{x}_2=36,5g;s_1=6,73g< 10g=s_2\). Suy ra trứng gà ở ổ thứ nhất đồng đều hơn.

C1:
\(A=\dfrac{10^{50}+2}{10^{50}-1}=\dfrac{10^{50}-1}{10^{50}-1}+\dfrac{3}{10^{50}-1}=1+\dfrac{3}{10^{50}-1}\\ B=\dfrac{10^{50}}{10^{50}-3}=\dfrac{10^{50}-3}{10^{50}-3}+\dfrac{3}{10^{50}-3}=1+\dfrac{3}{10^{50}-3}\\ \text{Vì }10^{50}-3< 10^{50}-1\Rightarrow\dfrac{3}{10^{50}-3}>\dfrac{3}{10^{50}-1}\Rightarrow1+\dfrac{3}{10^{50}-3}>1+\dfrac{3}{10^{50}-1}\Leftrightarrow B>A\)
Vậy \(B>A\)
C2: Áp dụng \(\dfrac{a}{b}>1\Rightarrow\dfrac{a}{b}>\dfrac{a+n}{b+n}\left(n>0\right)\)
Dễ thấy
\(B=\dfrac{10^{50}}{10^{50}-3}>1\\ \Rightarrow B=\dfrac{10^{50}}{10^{50}-3}>\dfrac{10^{50}+2}{10^{50}-3+2}=\dfrac{10^{50}+2}{10^{50}-1}=A\)
Vậy \(B>A\)
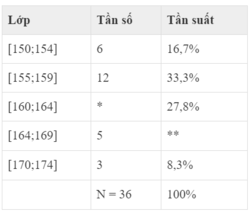






Dựa vào bảng phân bố tần số, tần suất ghép lớp ta có:
a) Giá trị của * là:
Đáp án: B
b) Giá trị của ** là:
Đáp án C