Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
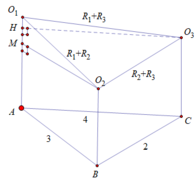
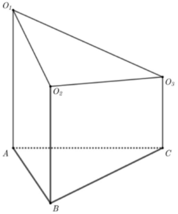
Không mất tính tổng quát, giả sử các đoạn thẳng có độ dài như hình vẽ:
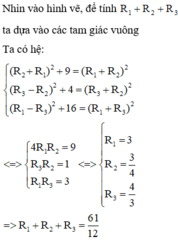
Gọi O1, O2, O3 lần lượt là tâm của ba mặt cầu đã cho và bán kính tương ứng là x, y,z ta có điều kiện các mặt cầu đôi một tiếp xúc ngoài là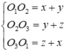 
và điều kiện tiếp xúc với mặt phẳng
(ABC) là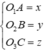 
Vậy theo pitago có
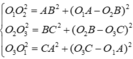
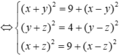
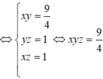
Chọn đáp án A.
Đáp án A.
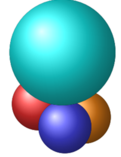
Bốn tâm của các bi nhỏ cùng với tâm của các bi lớn tạo thành hình chóp tứ giác đều có cạnh đáy bằng 2 và cạnh bên bằng 3. Khi đó chiều cao của hình chóp đều này là 7 .
Khoảng cách từ tâm của bi lớn đến đáy của hình hộp là 7 + 1 .
Do đó chiều cao của hình hộp là 2 . 7 + 1 = 2 + 2 7 .
Đáp án A.
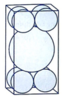
Bốn tâm của các bi nhỏ cùng với tâm của các bi lớn tạo thành hình chóp tứ giác đều có cạnh đáy bằng 2 và cạnh bên bằng 3. Khi đó chiều cao của hình chóp đều này là 7 .
Khoảng cách từ tâm của bi lớn đến đáy của hình hộp là 7 + 1 .
Do đó chiều cao của hình hộp là 2. 7 + 1 = 2 + 2 7 .
hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m
vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b
Đáp án C
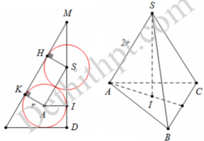
Gọi S, A, B, C lần lượt là tâm của các mặt cầu thứ tư và ba mặt cầu tiếp xúc đáy (như hình vẽ)
Khi đó S.ABC là khối tứ diện đều cạnh 2r.
Goi I là tâm của tam giác A B C ⇒ S i ⊥ A B C .
Tam giác ABC đều cạnh 2 r ⇒ A I = 2 r 3 .
Tam giác SAI vuông tại I, có S I = S A 2 − I A 2 = 4 r 2 − 2 r 3 2 = 2 6 3 r .
Ta thấy rằng Δ S M H ~ A S I g . g suy ra
S M S A = S H A I ⇒ S M = S A . A H A N = 2 r . r 2 r 3 = r 3 .
Vậy chiều cao của khối nón là h = S M + S I + I D = r 3 + 2 6 3 r + r = r 1 + 3 + 2 6 3 .
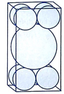
Đáp án là B
Gọi O 1 ; O 2 ; O 3 lần lượt là tâm của 3 mặt cầu và A ,B,C lần lượt là hình chiếu của 3 tâm trên mặt phẳng đã cho.
Suy ra:
A H = R 2 ; O 1 H = R 1 − R 2 ; O 2 H = A B ;
O 1 O 2 = R 1 + R 2
Xét tam giác vuông O 1 O 2 H: O 1 O 2 2 = O 1 H 2 + A B 2
⇒ R 1 + R 2 2 = R 1 − R 2 2 + A B 2
⇒ R 1 . R 2 = A B 2 4
Tương tự: R 2 . R 3 = B C 2 4 ; R 1 . R 3 = A C 2 4 ⇒ R 1 . R 2 . R 3 = 3