
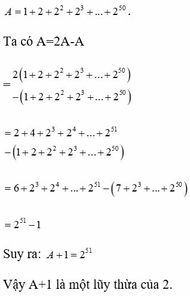
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

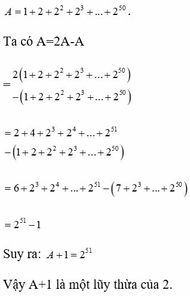

A=4+22+23+...+220
Đặt B=22+23+...+220
=>2B=23+24+...+221
=>2B-B=221-22=221-4
=>A=4+B=4+221-4=221
=>A là lũy thừa của 2(ĐPCM)
b)A=3+32+33+...+3100
=>3A=32+33+...+3101
=>3A-A=3101-3
=>2A=3101-3
=>2A+3=3101-3+3=3101
Vậy 2A+3 là lũy thừa của 3(ĐPCM)

\(S=1+2+2^2+...+2^{99}\)
\(2S=2+2^2+2^3+...+2^{100}\)
\(2S-S=\left(2+2^2+2^3+...+2^{100}\right)-\left(1+2+2^2+...+2^{99}\right)\)
\(S=2^{100}-1\)
\(A=S+1=2^{100}-1+1=2^{100}\left(ĐPCM\right)\)
\(A=S+1\)\(với\)\(S=1+2^1+2^2+...+2^{99}\)
- Xét S = 1 + 21 + 22 +...+ 299
=> 2.S = 2 + 22 + 23 +...+ 2100
=> 2.S - S = 2100 - 1
=> S = 2100 - 1
* A = S + 1 = 2100 - 1 + 1
=> A = 2100
Vậy A là một lũy thừa của 2 (Điều phải chứng minh)

Ta có :
\(S=1+3+3^2+3^3+..........+3^{99}\)
\(\Rightarrow3S=3+3^2+3^3+3^4+...................+3^{99}+3^{100}\)
\(\Rightarrow3S-S=\left(3+3^2+3^3+............+3^{100}\right)-\left(1+3+3^2+..........+3^{99}\right)\)
\(\Rightarrow2S=3^{100}-1\)
\(\Rightarrow2S+1=3^{100}-1+1=3^{100}\)
\(\Rightarrow2S+1\) là lũy thừa của \(3\)

a) M = 1 + 2 + 22 + 23 + ..... + 22019
= ( 1 + 2 + 4 ) + 23( 1 + 2 + 4 ) +.... + 22016 ( 1 + 2 + 4 )
= 7 ( 1 + 23 + 22016 ) chia hết cho 7 (đpcm)
b) M + 1 = 1 + 1 + 2 + 22 + 23 +... + 22019
= 4 + 22 + 2 3 + .....22019
= 2 x 22 + 23 + .... + 22019
= 2 x 23 + .... + 22019
= 2 x 2 2019
= 22020

Câu 1: ta có:
\(4C=4^2+4^3+...+4^n+4^{n+1}\)lấy 4C-C ta có:\(3C=4^{n+1}-4\)
=> C=\(\frac{4^{n+1}-4}{3}\)
b, tương tự ta có: \(5D=5+5^2+...+5^{2000}+5^{2001}\)
=> D=\(\frac{5^{2001}-1}{4}\)
Câu 2: ta có: \(2A=2+2^2+2^3+...+2^{200}+2^{201}\)
=> Lấy 2A - A, ta có: \(A=2^{201}-1\)=> A+1=2201 -1+1=2201 .
Vậy \(A+1=2^{201}\)
Câu 3: Ta có: \(3B=3^2+3^3+3^4+...+3^{2005}+3^{2006}\)
=> \(B=\frac{3^{2006}-3}{2}\)=> \(2B+3=3^{2006}-3+3=3^{2006}\)
Vậy 2B + 3 là một lũy thừa của 3...
Câu 4: Do 4=22nên ta có: \(2C=2^3+2^3+2^4+...+2^{2005}+2^{2006}\)
=> \(C=2^{2006}+2^3-\left(2^2+4\right)\)=>\(C=2^{2006}\)
Vậy C là lũy thừa của 2 có số mũ là 2006
Câu 5: a, Do 3n+2 chia hết cho n-1 hay:
3n-3+5 sẽ chia hết cho n-1 =>3(n-1) +5 chia hết cho n-1...mà 3(n-1) chia hết cho n-1 nên 5 chia hết n-1;
=> n-1 thuộc (1,5,-1,-5);;; nên n tương ứng với(2;6;0;-4)
b ,Do n+6 chia hết cho n nên 6 chia hết cho n hay n là ước của 6
nên => n thuộc (1,6,-1,-6);
c, Do 3n+4 chia hết cho n-1 hay: 3n-3+7 chia hết cho n-1
=> 3(n-1)+7 chia hết cho n-1 => 7 chia hết cho n-1;
n -1 thuộc (1,7,-1,-7) hay n sẽ tương ứng với( 2,8,0,-6);
d, Do n+5 chia hết cho n+1 hay n+1+4 chia hết cho n+1
=> 4 chia hết cho n+1 => n+1 thuộc (1,4,-1,-4) nên n tương ứng với (0,3,-2,-5);

A =4+2^2+2^3+...+2^50
A*2=2^3+2^3+2^4+...+2^50+2^51
A=(2^3+2^51)-(2^2+2^2)
A=8+2^51-8
A=2^51

a, M = 52+53+...+52014
5M = 53+54+...+52015
5M - M = 52015 - 52
4M = 52015 - 25
=> 4M + 25 = 52015 là một lũy thừa (đpcm)
b, 4M = 52015 - 25
=> M = \(\frac{5^{2015}-25}{4}<\frac{5^{2015}}{4}\)
=> M < \(\frac{5^{2015}}{4}\)

Ta có :
\(A=3+3^2+3^3+...+3^{100}\)
\(\Leftrightarrow\)\(3A=3^2+3^3+3^4+...+3^{101}\)
\(\Leftrightarrow\)\(3A-A=\left(3^2+3^3+3^4+...+3^{101}\right)-\left(3+3^2+3^3+...+3^{100}\right)\)
\(\Leftrightarrow\)\(2A=3^{101}-3\)
\(\Leftrightarrow\)\(A=\frac{3^{101}-3}{2}\)
\(\Rightarrow\)\(2A+3=\frac{3^{101}-3}{2}.2+3=3^{101}-3+3=3^{101}\)
Vì \(3^{101}\) là một luỹ thừa của \(3\)nên \(2A+3\) là một luỹ thừa của \(3\)
Vậy \(2A+3\)laf một luỹ thừa của \(3\)
\(A=3+3^2+......+3^{100}\)
\(\Leftrightarrow3A=3^2+3^3+.....+3^{101}\)
\(\Leftrightarrow3A-A=\left(3^2+3^3+.....+3^{101}\right)-\left(3+3^2+...+3^{100}\right)\)
\(\Leftrightarrow2A=3^{101}-3\)
\(\Leftrightarrow2A+3=3^{101}\)
\(\Leftrightarrow2A+3\) là 1 lũy thừ của 3