
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

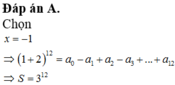

lim (x-->0) \(\frac{\sqrt[3]{ax+1}-\sqrt{1-bx}}{x}=2\)
<=> lim ( x-->0) \(\left(\frac{\sqrt[3]{ax+1}-1}{x}+\frac{1-\sqrt{1-bx}}{x}\right)=2\)
<=> lim (x-->0)\(\left(\frac{a}{\sqrt[3]{\left(ax+1\right)^2}+\sqrt[3]{ax+1}+1}+\frac{b}{\sqrt{1-bx}+1}\right)=2\)
<=> \(\frac{a}{3}+\frac{b}{2}=2\)
mà a + 3b = 3
=> a= 3; b = 2
=> A là đáp án sai.

\(\lim\limits_{x\rightarrow0}\frac{2\sqrt{1+x}-2+2-\sqrt[3]{8-x}}{x}=\lim\limits_{x\rightarrow0}\frac{\frac{2x}{\sqrt{1+x}+1}+\frac{x}{4+2\sqrt[3]{8-x}+\sqrt[3]{\left(8-x\right)^2}}}{x}\)
\(=\lim\limits_{x\rightarrow0}\left(\frac{2}{\sqrt{1+x}+1}+\frac{1}{4+2\sqrt[3]{8-x}+\sqrt[3]{\left(8-x\right)^2}}\right)=\frac{2}{2}+\frac{1}{4+4+4}=\frac{13}{12}\)

a) cosx - √3sinx = √2 ⇔ cosx - tan![]() sinx = √2
sinx = √2
⇔ cos![]() cosx - sin
cosx - sin![]() sinx = √2cos
sinx = √2cos![]() ⇔ cos(x +
⇔ cos(x + ![]() ) =
) = ![]()
⇔ 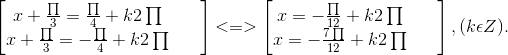
b) 3sin3x - 4cos3x = 5 ⇔ ![]() sin3x -
sin3x - ![]() cos3x = 1.
cos3x = 1.
Đặt α = arccos![]() thì phương trình trở thành
thì phương trình trở thành
cosαsin3x - sinαcos3x = 1 ⇔ sin(3x - α) = 1 ⇔ 3x - α = ![]() + k2π
+ k2π
⇔ x = ![]() , k ∈ Z (trong đó α = arccos
, k ∈ Z (trong đó α = arccos![]() ).
).

Lời giải:
\(\lim\limits _{x\to 0}\frac{(x+a)^3-a^3}{x}=\lim\limits _{x\to 0}\frac{x[(x+a)^2+a(x+a)+a^2]}{x}=\lim\limits _{x\to 0}[(x+a)^2+a(x+a)+a^2]\)
\(=3a^2\)
Để \(\lim\limits _{x\to 0}\frac{(x+a)^3-a^3}{x}=a\) \(\Leftrightarrow 3a^2=a\)
\(\Leftrightarrow 3a^2-a=0\Leftrightarrow a=0; a=\frac{1}{3}\) (có 2 giá trị thực của a)
Đáp án A.

16.
\(y'=\frac{\left(cos2x\right)'}{2\sqrt{cos2x}}=\frac{-2sin2x}{2\sqrt{cos2x}}=-\frac{sin2x}{\sqrt{cos2x}}\)
17.
\(y'=4x^3-\frac{1}{x^2}-\frac{1}{2\sqrt{x}}\)
18.
\(y'=3x^2-2x\)
\(y'\left(-2\right)=16;y\left(-2\right)=-12\)
Pttt: \(y=16\left(x+2\right)-12\Leftrightarrow y=16x+20\)
19.
\(y'=-\frac{1}{x^2}=-x^{-2}\)
\(y''=2x^{-3}=\frac{2}{x^3}\)
20.
\(\left(cotx\right)'=-\frac{1}{sin^2x}\)
21.
\(y'=1+\frac{4}{x^2}=\frac{x^2+4}{x^2}\)
22.
\(lim\left(3^n\right)=+\infty\)
11.
\(\lim\limits_{x\rightarrow1^+}\frac{-2x+1}{x-1}=\frac{-1}{0}=-\infty\)
12.
\(y=cotx\Rightarrow y'=-\frac{1}{sin^2x}\)
13.
\(y'=2020\left(x^3-2x^2\right)^{2019}.\left(x^3-2x^2\right)'=2020\left(x^3-2x^2\right)^{2019}\left(3x^2-4x\right)\)
14.
\(y'=\frac{\left(4x^2+3x+1\right)'}{2\sqrt{4x^2+3x+1}}=\frac{8x+3}{2\sqrt{4x^2+3x+1}}\)
15.
\(y'=4\left(x-5\right)^3\)

3.
\(x-2y+1=0\Leftrightarrow y=\frac{1}{2}x+\frac{1}{2}\)
\(y'=\frac{2}{\left(x+1\right)^2}\Rightarrow\frac{2}{\left(x+1\right)^2}=\frac{1}{2}\)
\(\Rightarrow\left(x+1\right)^2=4\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=1\\x=-3\Rightarrow y=3\end{matrix}\right.\)
Có 2 tiếp tuyến: \(\left[{}\begin{matrix}y=\frac{1}{2}\left(x-1\right)+1\\y=\frac{1}{2}\left(x+3\right)+3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}y=\frac{1}{2}x+\frac{1}{2}\left(l\right)\\y=\frac{1}{2}x+\frac{9}{2}\end{matrix}\right.\)
4.
\(\lim\limits\frac{\sqrt{2n^2+1}-3n}{n+2}=\lim\limits\frac{\sqrt{2+\frac{1}{n^2}}-3}{1+\frac{2}{n}}=\sqrt{2}-3\)
\(\Rightarrow\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\)
5.
\(\lim\limits_{x\rightarrow a}\frac{2\left(x^2-a^2\right)+a\left(a+1\right)-\left(a+1\right)x}{\left(x-a\right)\left(x+a\right)}=\lim\limits_{x\rightarrow a}\frac{\left(x-a\right)\left(2x+2a\right)-\left(a+1\right)\left(x-a\right)}{\left(x-a\right)\left(x+a\right)}\)
\(=\lim\limits_{x\rightarrow a}\frac{\left(x-a\right)\left(2x+a-1\right)}{\left(x-a\right)\left(x+a\right)}=\lim\limits_{x\rightarrow a}\frac{2x+a-1}{x+a}=\frac{3a-1}{2a}\)
1.
\(f'\left(x\right)=-3x^2+6mx-12=3\left(-x^2+2mx-4\right)=3g\left(x\right)\)
Để \(f'\left(x\right)\le0\) \(\forall x\in R\) \(\Leftrightarrow g\left(x\right)\le0;\forall x\in R\)
\(\Leftrightarrow\Delta'=m^2-4\le0\Rightarrow-2\le m\le2\)
\(\Rightarrow m=\left\{-1;0;1;2\right\}\)
2.
\(f'\left(x\right)=\frac{m^2-20}{\left(2x+m\right)^2}\)
Để \(f'\left(x\right)< 0;\forall x\in\left(0;2\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-20< 0\\\left[{}\begin{matrix}m>0\\m< -4\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-\sqrt{20}< m< \sqrt{20}\\\left[{}\begin{matrix}m>0\\m< -4\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow m=\left\{1;2;3;4\right\}\)

a) Ta có:
sin(x+1)=23⇔[x+1=arcsin23+k2πx+1=π−arcsin23+k2π⇔[x=−1+arcsin23+k2πx=−1+π−arcsin23+k2π;k∈Zsin(x+1)=23⇔[x+1=arcsin23+k2πx+1=π−arcsin23+k2π⇔[x=−1+arcsin23+k2πx=−1+π−arcsin23+k2π;k∈Z
b) Ta có:
sin22x=12⇔1−cos4x2=12⇔cos4x=0⇔4x=π2+kπ⇔x=π8+kπ4,k∈Zsin22x=12⇔1−cos4x2=12⇔cos4x=0⇔4x=π2+kπ⇔x=π8+kπ4,k∈Z
c) Ta có:
cot2x2=13⇔⎡⎢⎣cotx2=√33(1)cotx2=−√33(2)(1)⇔cotx2=cotπ3⇔x2=π3+kπ⇔x=2π3+k2π,k∈z(2)⇔cotx2=cot(−π3)⇔x2=−π3+kπ⇔x=−2π3+k2π;k∈Zcot2x2=13⇔[cotx2=33(1)cotx2=−33(2)(1)⇔cotx2=cotπ3⇔x2=π3+kπ⇔x=2π3+k2π,k∈z(2)⇔cotx2=cot(−π3)⇔x2=−π3+kπ⇔x=−2π3+k2π;k∈Z
d) Ta có:
tan(π12+12x)=−√3⇔tan(π12+12π)=tan(−π3)⇔π12+12=−π3+kπ⇔x=−5π144+kπ12,k∈Z
Vậy nghiệm của phương trình đã cho là: x=−5π144+kπ12,k∈Z
a)
\(sin\left(x+1\right)=\dfrac{2}{3}\Leftrightarrow\left[{}\begin{matrix}x+1=arcsin\dfrac{2}{3}+k2\pi\\x+1=\pi-arcsin\dfrac{2}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=arcsin\dfrac{2}{3}-1+k2\pi\\x=\pi-arcsin\dfrac{2}{3}-1+k2\pi\end{matrix}\right.\)\(\left(k\in Z\right)\).